
分析 过A作AD⊥BC于D(或延长线于D),根据含30度角的直角三角形的性质得到AD的长,再根据勾股定理得到BD,CD的长,再分两种情况:如图1,当AD在△ABC内部时、如图2,当AD在△ABC外部时,进行讨论即可求解.
解答 解:①如图1,作AD⊥BC,垂足为点D,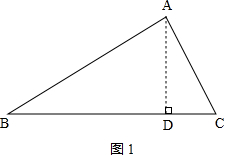
在Rt△ABD中,∵AB=12、∠B=30°,
∴AD=$\frac{1}{2}$AB=6,BD=ABcosB=12×$\frac{\sqrt{3}}{2}$=6$\sqrt{3}$,
在Rt△ACD中,CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{(\sqrt{39})^{2}-{6}^{2}}$=$\sqrt{3}$,
∴BC=BD+CD=6$\sqrt{3}$+$\sqrt{3}$=7$\sqrt{3}$,
则S△ABC=$\frac{1}{2}$×BC×AD=$\frac{1}{2}$×7$\sqrt{3}$×6=21$\sqrt{3}$;
②如图2,作AD⊥BC,交BC延长线于点D,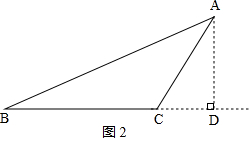
由①知,AD=6、BD=6$\sqrt{3}$、CD=$\sqrt{3}$,
则BC=BD-CD=5$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$×BC×AD=$\frac{1}{2}$×5$\sqrt{3}$×6=15$\sqrt{3}$,
故答案为:21$\sqrt{3}$或15$\sqrt{3}$.
点评 本题主要考查了解直角三角形,勾股定理,本题关键是得到BC和AD的长,同时注意分类思想的运用.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | $5\sqrt{3}π$ | B. | $5\sqrt{3}$ | C. | $3\sqrt{3}π$ | D. | $3\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | -3 | C. | 5 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
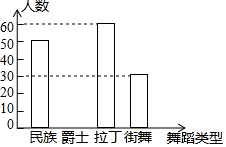 某校在艺术节选拔节目过程中,从备选的“街舞”、“爵士”、“民族”、“拉丁”四种类型舞蹈中,选择一种学生最喜爱的舞蹈,为此,随机调查了本校的部分学生,并将调查结果绘制成如下统计图表(每位学生只选择一种类型),根据统计图表的信息,解答下列问题:
某校在艺术节选拔节目过程中,从备选的“街舞”、“爵士”、“民族”、“拉丁”四种类型舞蹈中,选择一种学生最喜爱的舞蹈,为此,随机调查了本校的部分学生,并将调查结果绘制成如下统计图表(每位学生只选择一种类型),根据统计图表的信息,解答下列问题:| 类型 | 民族 | 拉丁 | 爵士 | 街舞 |
| 据点百分比 | a | 30% | b | 15% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,D为$\widehat{AC}$的中点,连接OD交弦AC于点F,过点D作DE∥AC,交BA的延长线于点E.
如图,AB为⊙O的直径,D为$\widehat{AC}$的中点,连接OD交弦AC于点F,过点D作DE∥AC,交BA的延长线于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com