

分析 (1)根据矩形的性质和已知条件得出∠HAE=45°,再根据HA=HG,得出∠HAE=∠HGA,从而得出答案;
(2)先分两种情况讨论:第一种情况,根据(1)得出∠AHG=90°,再根据折叠的性质得出∠HAE=∠F=45°,∠AHE=∠FHE,再根据EF∥HG,得出∠AHF=∠AHG-∠FHG,即可得出∠AHE=22.5°,此时,当B与G重合时,a的值最小,求出最小值;第二种情况:根据已知得出∠AEH+∠FEH=45°,由折叠的性质求出∠AHE的度数,此时,当B与E重合时,a的值最小,设DH=DA=x,则AH=GH=$\sqrt{2}$x,在Rt△AHG中,∠AHG=90°,根据勾股定理得:AG=$\sqrt{2}$AH=2x,再根据∠AEH=∠FEH,∠GHE=∠FEH,求出∠AEH=∠GHE,得出AB=AE=2x+$\sqrt{2}$x,从而求出a的最小值.
解答 解:(1)∵四边形ABCD是矩形,
∴∠ADH=90°,
∵DH=DA,
∴∠DAH=∠DHA=45°,
∴∠HAE=45°,
∵HA=HG,
∴∠HAE=∠HGA=45°;
故答案为:45.
(2)分两种情况讨论: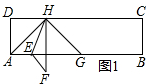
第一种情况:
∵∠HAG=∠HGA=45°;
∴∠AHG=90°,
由折叠可知:∠HAE=∠F=45°,∠AHE=∠FHE,
∵EF∥HG,
∴∠FHG=∠F=45°,
∴∠AHF=∠AHG-∠FHG=45°,
即∠AHE+∠FHE=45°,
∴∠AHE=22.5°,
此时,当B与G重合时,a的值最小,H为DC中点,DA=DH=$\frac{1}{2}$DC=$\frac{1}{2}$AB,
此时$\frac{AB}{AD}$=a=2,所以a的最小值是2;
第二种情况:
∵EF∥HG,
∴∠HGA=∠FEA=45°,
即∠AEH+∠FEH=45°,
由折叠可知:∠AEH=∠FEH,
∴∠AEH=∠FEH=22.5°,
∵EF∥HG,
∴∠GHE=∠FEH=22.5°,
∴∠AHE=90°+22.5°=112.5°,
此时,当B与E重合时,a的值最小,
设DH=DA=x,则AH=GH=$\sqrt{2}$x,
在Rt△AHG中,∠AHG=90°,由勾股定理得:
AG=$\sqrt{2}$AH=2x,
∵∠AEH=∠FEH,∠GHE=∠FEH,
∴∠AEH=∠GHE,
∴GH=GE=$\sqrt{2}$x,
∴AB=AE=2x+$\sqrt{2}$x,
∴a的最小值是$\frac{2x+\sqrt{2}x}{x}$=2+$\sqrt{2}$.
点评 此题考查了四边形的综合,用到的知识点是矩形的性质、折叠的性质、勾股定理等知识点,能够全面的思考问题,分类讨论求出∠AHE的度数,并求此时a的最小值是本题的难点.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
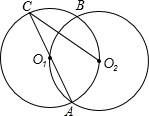 如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心O2,连接AO1,并延长交⊙O1于点C,则∠ACO2的度数为( )
如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心O2,连接AO1,并延长交⊙O1于点C,则∠ACO2的度数为( )| A. | 60° | B. | 45° | C. | 30° | D. | 20° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形ABCD中,点M为DA延长线上一点,连接BM,过点C作CN∥BM,交AD于点N,在CD延长线上取一点F,使BM=CF-DN,连接BF,交CN于点E.
如图,正方形ABCD中,点M为DA延长线上一点,连接BM,过点C作CN∥BM,交AD于点N,在CD延长线上取一点F,使BM=CF-DN,连接BF,交CN于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线y=$\frac{\sqrt{3}}{3}$x+2与x轴,y轴分别交于A,B两点,把△AOB沿着直线AB翻折后得到△AO′B,则点O′的坐标是( )
如图,直线y=$\frac{\sqrt{3}}{3}$x+2与x轴,y轴分别交于A,B两点,把△AOB沿着直线AB翻折后得到△AO′B,则点O′的坐标是( )| A. | (-$\sqrt{3}$,3) | B. | ($\sqrt{3}$,$\sqrt{3}$) | C. | (2,2$\sqrt{3}$) | D. | (2$\sqrt{3}$,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
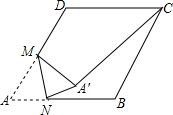 如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连结A′C,则A′C长度的最小值是( )
如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连结A′C,则A′C长度的最小值是( )| A. | $\sqrt{7}$ | B. | $\sqrt{7}-1$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点E为正方形ABCD边延长线上一点,AE交CD于F点,FG∥AD交DE于G点,其中有△ABE∽△FCE,△EFG∽△EAD,请探求CF与FG的大小关系,并说明理由.
如图,点E为正方形ABCD边延长线上一点,AE交CD于F点,FG∥AD交DE于G点,其中有△ABE∽△FCE,△EFG∽△EAD,请探求CF与FG的大小关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
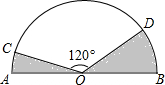 如图,已知C,D是以AB为直径的半圆周上的两点,O是圆心,半径OA=2,∠COD=120°,则图中阴影部分的面积等于$\frac{2}{3}$π.
如图,已知C,D是以AB为直径的半圆周上的两点,O是圆心,半径OA=2,∠COD=120°,则图中阴影部分的面积等于$\frac{2}{3}$π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com