
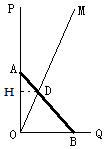
【题目】如图①,OP为一墙面,它与地面OQ垂直,有一根木棒AB如图放置,点C是它的中点,现在将木棒的A点在OP上由A点向下滑动,点B由O点向OQ方向滑动,直到AB横放在地面为止.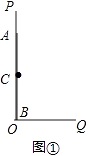
(1)在AB滑动过程中,点C经过的路径可以用下列哪个图象来描述( )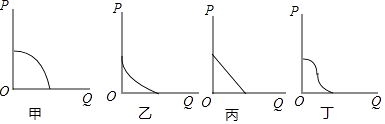
(2)若木棒长度为2m,如图②射线OM与地面夹角∠MOQ=60°,当AB滑动过程中,与OM并于点D,分别求出当AD= ![]() 、AD=1、AD=
、AD=1、AD= ![]() 时,OD的值.
时,OD的值.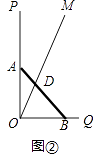
(3)如图③,是一个城市下水道,下水道入口宽40cm,下水道水平段高度为40cm,现在要想把整根木棒AB通入下水道水平段进行工作,那么这根木棒最长可以是(cm)(直接写出结果,结果四舍五入取整数).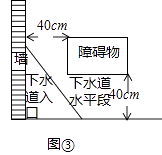
【答案】
(1)甲
(2)解:过D作DH⊥OP于H,设DH=a,在Rt△OHD中,
∵∠AOD=90°﹣600=300,
∴OD=2a,OH= ![]() a,
a,
∵DH⊥OA,OQ⊥OA,
∴DH∥QO,
∴ ![]() =
= ![]() ,
,
当AD= ![]() 时,BD=
时,BD= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AH= ![]() a,
a,
在Rt△AHD中,
∵AH2+DH2=AD2,
∴ ![]() a2+a2=
a2+a2= ![]() ,
,
解得a= ![]() ,OD=
,OD= ![]() ,
,
当AD=1时,BD=1,
∴ ![]() =
= ![]() ,
,
∴AH= ![]() a,
a,
在Rt△AHD中,∵AH2+DH2=AD2,
∴3a2+a2=1,
解得a= ![]() ,OD=1,
,OD=1,
当AD= ![]() 时,BD=
时,BD= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AH=2 ![]() a,
a,
在Rt△AHD中,∵AH2+DH2=AD2,
∴12a2+a2= ![]() ,
,
解得a= ![]() ,OD=
,OD= ![]()
(3)113
【解析】解:(1)∵点C是AB的中点,
∴OC= ![]() AB,
AB,
∴点C的运动轨迹是以O为圆心, ![]() AB长为半径的圆弧,经过的路程的
AB长为半径的圆弧,经过的路程的 ![]() 圆周.
圆周.
故选甲.(3)由题意当等腰直角三角形的直角边为80cm时,斜边为 ![]() ≈113cm,
≈113cm,
所以这根木棒最长可以是113cm.
所以答案是113cm.
【考点精析】解答此题的关键在于理解相似三角形的性质的相关知识,掌握对应角相等,对应边成比例的两个三角形叫做相似三角形.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】已知a,b,c是△ABC的三边,若a,b,c满足a2-6a+b2-8b+![]() +25=0,则△ABC是_____________三角形;若a,b,c满足a2+b2+c2-ab-bc-ac=0,则△ABC是_________三角形.
+25=0,则△ABC是_____________三角形;若a,b,c满足a2+b2+c2-ab-bc-ac=0,则△ABC是_________三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】遂宁市明星水利为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括最大值但不包括最小值),请你根据统计图解决下列问题:
(1)此次调查抽取了多少用户的用水量数据?
(2)补全左侧统计图,并求扇形统计图中“25吨~30吨”部分的圆心角度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
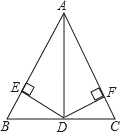
【题目】如图,在△ABC中,AD平分∠BAC交BC于D,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.
(1)求证:AB=AC;
(2)若DC=4,∠DAC=30°,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”所示我国的传统佳节,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销售较好的肉馅棕、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不用口味粽子的喜爱情况,在节前对某居民区进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整). 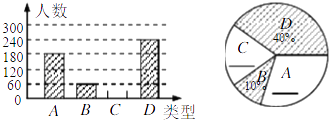
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个,用列表或画树状图的方法,求他第二个恰好吃到的是C粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?请列出二元一次方程组解答此问题.
(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置.1.设原来每天安排x名工人生产G型装置,后来补充m名新工人,求x的值(用含m的代数式表示)2.请问至少需要补充多少名新工人才能在规定期内完成总任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
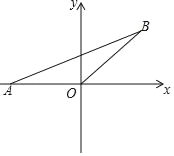
【题目】如图,等腰△AOB中,AO=BO=2,点A在x轴上,OB与x轴的夹角为45°;
(1)求直线AB、OB的解析式;
(2)若将△AOB沿着x轴翻折再向右平移两个单位求直线AB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张宽为6cm的平行四边形纸带ABCD如图1所示,AB=10cm,小明用这张纸带将底面周长为10cm直三棱柱纸盒的侧面进行包贴(要求包贴时没有重叠部分).小明通过操作后发现此类包贴问题可将直三棱柱的侧面展开进行分析.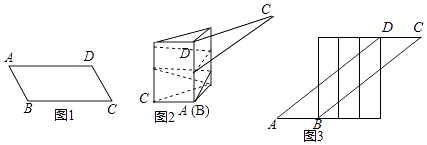
(1)若纸带在侧面缠绕三圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则纸带AD的长度为 cm;
(2)若AD=100cm,纸带在侧面缠绕多圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则这个直三棱柱纸盒的高度是 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知两点A(3,m),B(2m,4),且A和B到x轴距离相等,求B点坐标.
(2)点A在第四象限,当m为何值时,点A(m+2,3m5)到x轴的距离是它到y轴距离的一半.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com