
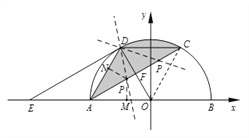
【题目】如图, ![]() 为
为![]() 的直径,
的直径, ![]() 为弦
为弦![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ∥
∥![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,
, ![]() .
.

(1)求证: ![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() 时,
时,
①求图中阴影部分的面积;
②以![]() 为原点,
为原点, ![]() 所在的直线为
所在的直线为![]() 轴,直径
轴,直径![]() 的垂直平分线为
的垂直平分线为![]() 轴,建立如图所示的平面直角坐标系,试在线段
轴,建立如图所示的平面直角坐标系,试在线段![]() 上求一点
上求一点![]() ,使得直线
,使得直线![]() 把阴影部分的面积分成
把阴影部分的面积分成![]() 的两部分.
的两部分.
【答案】(1)证明见解析;(2) ①![]() ②
②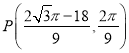 或
或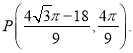
【解析】试题分析:(1)、连接OC,根据等腰三角形的三线合一定理得出OD⊥AC,根据平行线的性质得出OD⊥DE,从而得出切线;(2)、首先得出△AOD为等边三角形,然后根据题意得出△ACD和△OCD的面积相等,从而得出阴影部分的面积等于扇形OCD的面积,然后根据扇形的面积计算法则得出答案;(3)、根据题意得出直线AC的解析式,过点P分别作PM⊥x轴,PN⊥AD,垂足分别为M,N,设设![]() 根据面积分成1:2两部分得出△APD的面积等于阴影部分面积的
根据面积分成1:2两部分得出△APD的面积等于阴影部分面积的![]() 或
或![]() 列出方程,求出x的值,得出点P的坐标.
列出方程,求出x的值,得出点P的坐标.
试题解析:(1)、连结![]() ∵
∵![]()
![]() 为
为![]() 的中点 ∴
的中点 ∴![]() 又∵
又∵![]()
∴![]() ∴
∴![]() 是⊙O的切线
是⊙O的切线
(2)、①由(1)得![]() ∴
∴![]() ∴
∴![]() ∴
∴![]()
∴![]() ∴
∴![]() 是等边三角形 ∴
是等边三角形 ∴![]()
∴![]() 又∵
又∵![]() ∴
∴![]()
∴![]() ∴
∴![]()
∴![]() ∴
∴![]() ∵
∵![]()
∴![]() ∴
∴![]()
②由已知得: ![]() ∴直线
∴直线![]() 的表达式为
的表达式为![]()
过点P分别作![]() 轴,
轴, ![]() 垂足分别为
垂足分别为![]() ,
, ![]() , 由①得
, 由①得![]() 平分
平分![]()
∴![]() 设
设![]()
![]() ∵直线
∵直线![]() 把阴影部分的面积分成
把阴影部分的面积分成![]() 的两部分
的两部分
若![]() 即
即![]()
解得: ![]() ,此时
,此时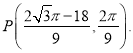
若![]() 同理可求得
同理可求得
综上所述:满足条件的点P的坐标为 和
和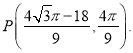


科目:初中数学 来源: 题型:
【题目】将纸片△ABC沿DE折叠使点A落在A′处的位置.
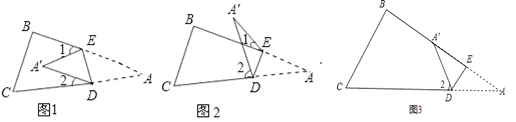
(1)如果A′落在四边形BCDE的内部(如图1),∠A′与∠1+∠2之间存在怎样的数量关系?并说明理由.
(2)如果A′落在四边形BCDE的BE边上,这时图1中的∠1变为0°角,(如图3)则∠A′与∠2之间的关系是 .
(3)如果A′落在四边形BCDE的外部(如图2),这时∠A′与∠1、∠2之间又存在怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
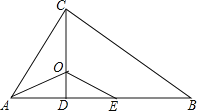
【题目】如图,△ABC中,∠ACB=90°,CD⊥AB于点D,AO平分∠BAC,交CD于点O,E为AB上一点,且AE=AC。
(1)求证:△AOC≌△A0E;
(2)求证:OE∥BC。
查看答案和解析>>
科目:初中数学 来源: 题型:
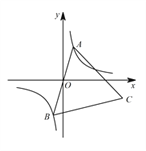
【题目】如图,已知点 ![]() 是双曲线
是双曲线 ![]() 在第三象限分支上的一个动点,连接
在第三象限分支上的一个动点,连接 ![]() 并延长交另一分支于点
并延长交另一分支于点 ![]() ,以
,以 ![]() 为边作等边三角形
为边作等边三角形 ![]() ,点
,点 ![]() 在第四象限内,且随着点
在第四象限内,且随着点 ![]() 的运动,点
的运动,点 ![]() 的位置也在不断变化,但点
的位置也在不断变化,但点 ![]() 始终在双曲线
始终在双曲线 ![]() 上运动,则
上运动,则 ![]() 的值是_______________.
的值是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
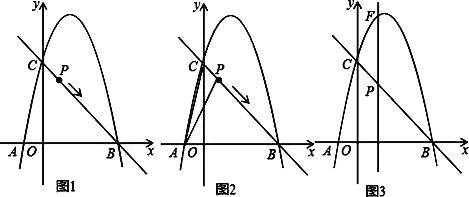
【题目】如图1,抛物线y=ax2+bx+5的图象过A(﹣1,0),B(5,0)两点,与y轴交于点C,作直线BC,动点P从点C出发,以每秒![]() 个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.
个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.
(1)求抛物线的表达式;
(2)如图2,当t=1时,若点Q是X轴上的一个动点,如果以Q,P,B为顶点的三角形与△ABC相似,求出Q点的坐标;
(3)如图3,过点P向x轴作垂线分别交x轴,抛物线于E、F两点.
①求PF的长度关于t的函数表达式,并求出PF的长度的最大值;
②连接BF,将△PBF沿BF折叠得到△P′BF,当t为何值时,四边形PFP′B是菱形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国政府从2007年起对职业中专在校生给予生活补贴,每位在校生每年补贴1500元某市预计2008年职业中专在校生人数是2007年的1.2倍,于是要在2007年的基础上增加补贴600万元。2008年该市职业中专在校生有多少万人?补贴多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
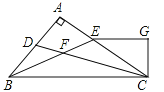
【题目】如图,△ABC的角平分线 CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=![]() ∠CGE.
∠CGE.
其中正确的结论是_____________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是( )

A. ∠A+∠C+∠D+∠E=360°
B. ∠A+∠D=∠C+∠E
C. ∠A-∠C+∠D+∠E=180°
D. ∠E-∠C+∠D-∠A=90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com