
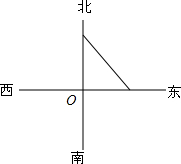
 如图所示,东西和南北街道交于点O,甲沿东西道由西向东走,速度是每秒4m,乙沿南北道由南向北走,速度是每秒3m,当乙通过O点后又继续前进50m时,甲刚好通过O点,当甲、乙相距85m时,求每个人的位置.
如图所示,东西和南北街道交于点O,甲沿东西道由西向东走,速度是每秒4m,乙沿南北道由南向北走,速度是每秒3m,当乙通过O点后又继续前进50m时,甲刚好通过O点,当甲、乙相距85m时,求每个人的位置. 分析 设甲通过O点x秒后,甲、乙相距85m;则OM=4xm,ON=(3x+50)m,由勾股定理得出方程,解方程求出x,得出OM、ON的长即可.
解答 解:设甲通过O点x秒后,甲、乙相距85m;如图所示:
则OM=4xm,ON=(3x+50)m,
由勾股定理得:OM2+ON2=MN2,
即(4x)2+(3x+50)2=852,
解得:x=9或x=-21,
当x=9时,OM=36米,ON=3×9+50=77(米),
当x=-21时,OM=-84米,ON=3×(-21)+50=13(米),
即当甲、乙相距85m时,甲在点O东36米,乙在点O北77米;或甲在点O西84米,乙在点O北13米.
点评 本题考查了勾股定理的应用;熟练掌握勾股定理,根据勾股定理列出方程是解决问题的关键.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
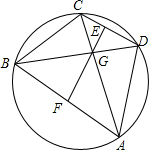 在圆内接四边形ABCD中,对角线AC⊥BD于G.
在圆内接四边形ABCD中,对角线AC⊥BD于G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com