
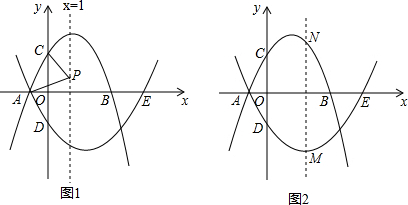
���� ��1���ɶԳ�������b�������l1�Ľ���ʽ����y=0�����A�����꣬�����ô���ϵ���������l2�ı���ʽ��
��2����P������Ϊ��1��y�����ɹ��ɶ����ɱ�ʾ��PC2��PA2���������ɵõ�����y�ķ��̿����y�������P�����ꣻ
��3���ɷֱ����M��N�����꣬�ɱ�ʾ��MN���ٸ��ݺ��������ʿ����MN�����ֵ��
��� �⣺��1����������l1��y=-x2+bx+3�ĶԳ���Ϊx=1��
��-$\frac{b}{-2}$=1�����b=2��
��������l1�Ľ���ʽΪy=-x2+2x+3��
��y=0���ɵ�-x2+2x+3=0�����x=-1��x=3��
��A��������-1��0����
��������l2������A��E���㣬
�����������l2����ʽΪy=a��x+1����x-5����
�֡�������l2��y���ڵ�D��0��-$\frac{5}{2}$����
��-$\frac{5}{2}$=-5a�����a=$\frac{1}{2}$��
��y=$\frac{1}{2}$��x+1����x-5��=$\frac{1}{2}$x2-2x-$\frac{5}{2}$��
��������l2�ĺ�������ʽΪy=$\frac{1}{2}$x2-2x-$\frac{5}{2}$��
��2����P������Ϊ��1��y�����ɣ�1���ɵ�C������Ϊ��0��3����
��PC2=12+��y-3��2=y2-6y+10��PA2=[1-��-1��]2+y2=y2+4��
��PC=PA��
��y2-6y+10=y2+4�����y=1��
��P��������1��1����
��3�����������M��x��$\frac{1}{2}$x2-2x-$\frac{5}{2}$����
��MN��y�ᣬ
��N��x��-x2+2x+3����$\frac{1}{2}$x2-2x-$\frac{5}{2}$
��-x2+2x+3=$\frac{1}{2}$x2-2x-$\frac{5}{2}$���ɽ��x=-1��x=$\frac{11}{3}$��
�ٵ�-1��x��$\frac{11}{3}$ʱ��MN=��-x2+2x+3��-��$\frac{1}{2}$x2-2x-$\frac{5}{2}$��=-$\frac{3}{2}$x2+4x+$\frac{11}{2}$=-$\frac{3}{2}$��x-$\frac{4}{3}$��2+$\frac{49}{6}$��
��Ȼ-1��$\frac{4}{3}$��$\frac{11}{3}$���൱x=$\frac{4}{3}$ʱ��MN�����ֵ$\frac{49}{6}$��
�ڵ�$\frac{11}{3}$��x��5ʱ��MN=��$\frac{1}{2}$x2-2x-$\frac{5}{2}$��-��-x2+2x+3��=$\frac{3}{2}$x2-4x-$\frac{11}{2}$=$\frac{3}{2}$��x-$\frac{4}{3}$��2-$\frac{49}{6}$��
��Ȼ��x��$\frac{4}{3}$ʱ��MN��x�����������
�൱x=5ʱ��MN�����ֵ��$\frac{3}{2}$����5-$\frac{4}{3}$��2-$\frac{49}{6}$=12��
���Ͽ�֪�ڵ�M�Ե�A�˶�����E�Ĺ����У��߶�MN���ȵ����ֵΪ12��
���� ������Ҫ������κ������ۺ�Ӧ�ã��漰����ϵ���������κ��������ʡ����ɶ�����֪ʶ�㣮�ڣ�1�������A��������ǽ���Ĺؼ����ڣ�2������P�������ֱ��ʾ��PA��PC�ǽ���Ĺؼ����ڣ�3������M��N������ֱ��ʾ��MN�ij��ǽ���Ĺؼ���ע��������ۣ����⿼��֪ʶ���Ϊ�������Ѷ����У�


 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a6��a2=a3 | B�� | a2+a2=a4 | C�� | ��a3��2=a6 | D�� | a3•a3=a9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
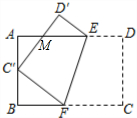 ��ͼ��������ABCD��EF�۵���ʹ����Cǡ������AB�ߵ��е�C���ϣ���D����D�䴦��C��D�佻AE�ڵ�M����AB=6��BC=9����AM�ij�Ϊ$\frac{9}{4}$��
��ͼ��������ABCD��EF�۵���ʹ����Cǡ������AB�ߵ��е�C���ϣ���D����D�䴦��C��D�佻AE�ڵ�M����AB=6��BC=9����AM�ij�Ϊ$\frac{9}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
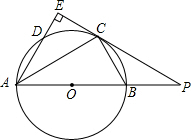 ��ͼ��AB�ǡ�O��ֱ������CΪ��O��һ�㣬AE����C�������ഹֱ������ΪE��AE����O�ڵ�D��ֱ��EC��AB���ӳ����ڵ�P������AC��BC��PB��PC=1��2��
��ͼ��AB�ǡ�O��ֱ������CΪ��O��һ�㣬AE����C�������ഹֱ������ΪE��AE����O�ڵ�D��ֱ��EC��AB���ӳ����ڵ�P������AC��BC��PB��PC=1��2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
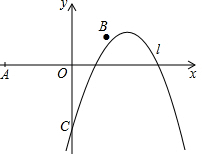 ��ͼ����֪��O��0��0����A��-5��0����B��2��1����������l��y=-��x-h��2+1��hΪ��������y��Ľ���ΪC��
��ͼ����֪��O��0��0����A��-5��0����B��2��1����������l��y=-��x-h��2+1��hΪ��������y��Ľ���ΪC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
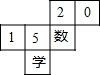 ��ͼ��һ��������ֽ�е�չ��ͼ�����е������������ڷֱ�������֡�0������1������2������5���ͺ��֡�����������ѧ��������Χ��һ������������롰5����Ե��ǣ�������
��ͼ��һ��������ֽ�е�չ��ͼ�����е������������ڷֱ�������֡�0������1������2������5���ͺ��֡�����������ѧ��������Χ��һ������������롰5����Ե��ǣ�������| A�� | 0 | B�� | 2 | C�� | �� | D�� | ѧ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | ������� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com