
 =
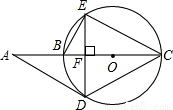
= ,可得:ED=CD,根据BC为⊙O的直径可知:∠BEC=90°,再根据∠BED的度数,可求得∠DEC=60°,从而可证:△DCE是等边三角形;
,可得:ED=CD,根据BC为⊙O的直径可知:∠BEC=90°,再根据∠BED的度数,可求得∠DEC=60°,从而可证:△DCE是等边三角形; 解:(1)连接OD,
解:(1)连接OD, ∠AOD=30°;
∠AOD=30°;
 ,
, =
= .
.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2007年全国中考数学试题汇编《二次函数》(08)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2007年全国中考数学试题汇编《反比例函数》(05)(解析版) 题型:解答题
 的图象交于A(-1,2),B(2,n)两点.
的图象交于A(-1,2),B(2,n)两点.
查看答案和解析>>
科目:初中数学 来源:2007年广西贵港市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2007年广西贵港市中考数学试卷(解析版) 题型:解答题
 的图象交于A(-1,2),B(2,n)两点.
的图象交于A(-1,2),B(2,n)两点.
查看答案和解析>>
科目:初中数学 来源:2007年全国中考数学试题汇编《图形的对称》(05)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com