
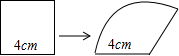
 手工课上,小明将一个边长为4cm的正方形铁丝框,变形成为如图所示一个扇形框,周长不变,且扇形框半径等于正方形的边长,则该扇形的面积大小为16cm2.
手工课上,小明将一个边长为4cm的正方形铁丝框,变形成为如图所示一个扇形框,周长不变,且扇形框半径等于正方形的边长,则该扇形的面积大小为16cm2.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
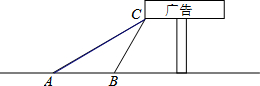 如图,某学校数学兴趣小组想了解“第25届世界技巧锦标赛倒计时”广告牌的高度,他们在A点处测得广告牌底端C点的仰角为30°,然后向广告牌前进10m到达点B处,又测得C点的仰角为60°.请你根据以上数据求广告牌底端C点离地面的高度.(结果保留根号)
如图,某学校数学兴趣小组想了解“第25届世界技巧锦标赛倒计时”广告牌的高度,他们在A点处测得广告牌底端C点的仰角为30°,然后向广告牌前进10m到达点B处,又测得C点的仰角为60°.请你根据以上数据求广告牌底端C点离地面的高度.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起,据试验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起,据试验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某大街水平地面有两根路灯灯杆AB=CD=10m,小明晚上站在两灯杆的正中位置观察自己眼睛处影子的俯角∠MEG=∠NEH=11.31°,已知地面到小明眼睛处的高度EF=1.5m.
如图,某大街水平地面有两根路灯灯杆AB=CD=10m,小明晚上站在两灯杆的正中位置观察自己眼睛处影子的俯角∠MEG=∠NEH=11.31°,已知地面到小明眼睛处的高度EF=1.5m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com