
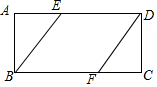
 如图,矩形ABCD中,AD=2AB,点E、F分别在AD、BC上,若四边形BFDE为菱形,则AE:ED的值为( )
如图,矩形ABCD中,AD=2AB,点E、F分别在AD、BC上,若四边形BFDE为菱形,则AE:ED的值为( )| A. | 1:2 | B. | 3:5 | C. | $\sqrt{2}$:3 | D. | 3:4 |
分析 由题意易得ED∥BF,AD=BC而AE=CF,那么可得到ED=BF,即可得出四边形BFDE是平行四边形.结合菱形的四条边相等来求AE的长度,得出DE,即可得出答案.
解答 解:∵四边形ABCD为矩形,
∴AD∥BC且AD=BC.
又∵AE=CF,
∴AD-AE=BC-CF,即ED=BF,
由ED∥BF且ED=BF,
∴四边形BEDF为平行四边形(一组对边平行且相等的四边形为平行四边形).
当BE=DE时,四边形BEDF为菱形
设AB=x,BE=DE=y,则AD=2x,AE=2x-y,
在直角△ABE中:x2+(2x-y)2=y2,
则:x=$\frac{4}{5}$y,
∴AE=2x-y=$\frac{3}{5}$y,
∴AE:ED=3:5
故选:B.
点评 本题综合应用了平行四边形的性质和判定,矩形和菱形的判定.要根据条件合理、灵活地选择方法.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
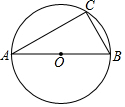 如图,⊙O是△ABC的外接圆,∠C=90°,sin∠A=$\frac{\sqrt{3}}{3}$,BC=2$\sqrt{3}$,则⊙O的半径为3.
如图,⊙O是△ABC的外接圆,∠C=90°,sin∠A=$\frac{\sqrt{3}}{3}$,BC=2$\sqrt{3}$,则⊙O的半径为3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
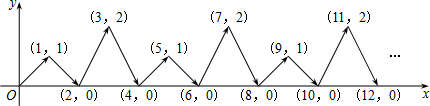
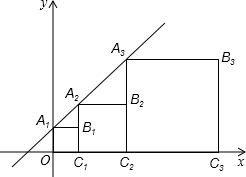 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示放置,点A1,A2,A3,和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1,B2,B3,B4的坐标分别为(1,1)(3,2),(7,4),(15,8),则Bn的坐标是( )
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示放置,点A1,A2,A3,和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1,B2,B3,B4的坐标分别为(1,1)(3,2),(7,4),(15,8),则Bn的坐标是( )| A. | (2n-1,2n-1) | B. | (2n,2n-1) | C. | (2n-1,2n) | D. | (2n-1-1,2n-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 平均数 | 标准差 | 中位数 | |
| 甲队 | 1.72 | 0.038 | 1.73 |
| 乙队 | 1.69 | 0.025 | 1.70 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,-3) | B. | (2,3) | C. | (3,-2) | D. | (-3,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 小鹏早晨到校发现作业忘带,就打电话叫爸爸立即把作业送到学校,小鹏也同时往家赶,两人相遇后,小鹏以原速度返回学校,爸爸则以原速度的$\frac{2}{3}$返回家.设爸爸行走的时间为x分钟,小鹏和爸爸两人之间的距离为y米,y与x的函数关系如图所示,则当小鹏回到学校时,爸爸还需要2.5分钟才能到家.
小鹏早晨到校发现作业忘带,就打电话叫爸爸立即把作业送到学校,小鹏也同时往家赶,两人相遇后,小鹏以原速度返回学校,爸爸则以原速度的$\frac{2}{3}$返回家.设爸爸行走的时间为x分钟,小鹏和爸爸两人之间的距离为y米,y与x的函数关系如图所示,则当小鹏回到学校时,爸爸还需要2.5分钟才能到家.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com