练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．某校甲、乙、丙、丁四名同学在运动会上参加4×100米接力比赛，其中甲跑第一棒，那么乙跑第二棒的概率为（　　）
    A．$\frac{1}{24}$B．$\frac{1}{12}$C．$\frac{1}{6}$D．$\frac{1}{3}$

    分析 直接根据概率公式即可得出结论．

    解答 解：∵甲跑第一棒，
    ∴跑第二棒的有三种可能：乙、丙、丁，
    ∴乙跑第二棒的概率=$\frac{1}{3}$．
    故选D．

    点评 本题考查的是概率公式，熟记随机事件的概率公式是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    11．一元二次方程x2-4x+3=0的根是（　　）
    A．-1B．-3C．1和3D．-1和-3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

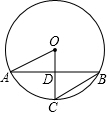    12．如图，⊙O的半径OC垂直于弦AB，垂足为D，OA=2$\sqrt{2}$，∠B=22.5°，AB的长为（　　）
    A．2B．4C．2$\sqrt{2}$D．4$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

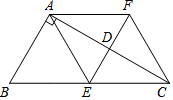    9．如图，在△ABC中，∠BAC=90°，线段AC的垂直平分线交AC于D点，交BC于E点，过点A作BC的平行线交直线ED于F点，连接AE，CF．
    （1）求证：四边形AECF是菱形；
    （2）若AB=10，∠ACB=30°，求菱形AECF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知抛物线y=ax2+bx+c（a≠0）经过点A（1，0），B（3，0），C（0，3）．

    （1）求抛物线的表达式及顶点D的坐标；
    （2）如图甲，点P是直线BC上方抛物线上一动点，过点P作y轴的平行线，交直线BC于点E，是否存在一点P，使线段PE的长最大？若存在，求出PE长的最大值；若不存在，请说明理由；
    （3）如图乙，过点A作y轴的平行线，交直线BC于点F，连接DA、DB四边形OAFC沿射线CB方向运动，速度为每秒1个单位长度，运动时间为t秒，当点C与点B重合时立即停止运动，设运动过程中四边形OAFC与四边形ADBF重叠部分面积为S，请求出S与t的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．先化简，再求值：（x+2）（x-2）-（x-1）2，其中x=-$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．高铁的开通，给N市市民出行带来了极大的方便，“元旦”期间，甲、乙两人应邀到A市的艺术馆参加演出，甲乘私家车从N市出发1小时后，乙乘坐高铁从N市出发，先到A市火车站，然后再转乘出租车到A市的艺术馆（换车时间忽略不计），两人恰好同时到达A市的艺术馆，他们离开N市的距离y（千米）与乘车时间x（小时）的关系如图所示，请结合图象解答下列问题：
    （1）高铁的平均速度是每小时多少千米？
    （2）分别求甲、乙（乘坐高铁时）两人离开N市的距离y与乘车时间x的函数关系式；
    （3）若甲要提前30分钟到达艺术馆，那么私家车的速度必须达到多少千米/小时？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．一个口袋中有三个完全相同的小球，把它们分别标号为123，随机地摸出一个小球，然后放回，再随机摸出一个小球，则两次摸出的小球标号的和等于4的概率是$\frac{1}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．某大学棋艺协会定期举办“以棋会友”的竞赛活动，包括“中国象棋”、“围棋”、“五子棋”、“国际象棋”四种比赛，每位协会会员必须参加其中的两种棋类比赛，且各队员之间参加比赛相互独立．已知甲同学必选“中国象棋”，不选“国际象棋”，乙同学从四种比赛中任选两种参与．
    （Ⅰ）求甲参加围棋比赛的概率；
    （Ⅱ）求甲、乙两人参与的两种比赛都不同的概率．

    查看答案和解析>>

    同步练习册答案