Question

如图，在△ABC中，∠BAC＝90°，AB＝AC＝6，D为BC的中点．

（1）若E、F分别是AB、AC上的点，且AE＝CF，求证：△AED≌△CFD；
（2）当点F、E分别从C、A两点同时出发，以每秒1个单位长度的速度沿CA、AB运动，到点A、B时停止；设△DEF的面积为y，F点运动的时间为x，求y与x的函数关系式；
（3）在（2）的条件下，点F、E分别沿CA、AB的延长线继续运动，求此时y与x的函数关系式．

Answer 1

（1）利用等腰直角三角形的性质得到∠BAD=∠DAC=∠B=∠C=45°，进而得到AD=BD=DC，为证明△AED≌△CFD提供了重要的条件；（2）；（3）

解析试题分析：（1）利用等腰直角三角形的性质得到∠BAD=∠DAC=∠B=∠C=45°，进而得到AD=BD=DC，为证明△AED≌△CFD提供了重要的条件；
（2）利用S_{四边形AEDF}=S_△AED+S_△ADF=S_△CFD+S_△ADF=S_△ADC="9" 即可得到y与x之间的函数关系式；
（3）依题意有：AF=BE=x-6，AD=DB，∠ABD=∠DAC=45°得到∠DAF=∠DBE=135°，从而得到△ADF≌△BDE，利用全等三角形面积相等得到S_△ADF=S_△BDE从而得到S_△EDF=S_△EAF+S_△ADB即可确定两个变量之间的函数关系式．
（1）∵∠BAC=90° AB=AC=6，D为BC中点
∴∠BAD=∠DAC=∠B=∠C=45°    
∴AD=BD=DC
∵AE=CF
∴△AED≌△CFD（SAS）    
（2）依题意有：FC=AE=x，
∵△AED≌△CFD
∴S_{四边形AEDF}=S_△AED+S_△ADF=S_△CFD+S_△ADF=S_△ADC=9     
∴S_△EDF=S_{四边形AEDF}-S_△AEF=9-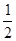(6-x)x=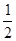x²-3x+9
∴；
（3）依题意有：AF=BE=x-6，AD=DB，∠ABD=∠DAC=45°
∴∠DAF=∠DBE=135°    
∴△ADF≌△BDE    
∴S_△ADF=S_△BDE
∴S_△EDF=S_△EAF+S_△ADB=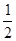(x-6)x+9=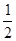x²-3x+9
∴．
考点：动点问题的综合题
点评：此类问题难度较大，在中考中比较常见，一般在压轴题中出现，需特别注意.