练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．如果-$\frac{x}{10}$=$\frac{y}{5}$，那么x=-2y，根据等式的性质2：等式两边乘同一个数或除以一个不为零的数，结果仍得等式．

    分析 根据等式的性质2：等式的两边同乘（或除以）同一个数（除数不为0）结果仍相等即可得出答案．

    解答 解：如果-$\frac{x}{10}$=$\frac{y}{5}$，那么x=-2y，根据等式的性质2：等式两边乘同一个数或除以一个不为零的数，结果仍得等式．
    故答案为：-2y，2：等式两边乘同一个数或除以一个不为零的数，结果仍得等式．

    点评 此题考查了等式的性质，掌握等式的性质是本题的关键，等式性质1：等式的两边加（或减）同一个数（或式子）结果仍相等；等式性质2：等式的两边同乘（或除以）同一个数（除数不为0）结果仍相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．先化简．再求值：（-$\frac{1}{3}$xy）2•[xy（2x-y）-2x（xy-y2）]，其中x=-$\frac{3}{2}$，y=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图（a），∠DAB+∠ABC+∠BCE=360°
    （1）求证：AD∥CE
    （2）如图（b），AG、CG分别平分∠BAD、∠BCE，BF∥AG交GC的延长线于F，判断∠ABC与∠F的数量关系，并证明；
    （3）如图（c），AN平分∠HAB，BP平分∠ABC，BQ∥AN，CM平分∠BCT交BQ的反向延长线于M，①$\frac{∠QBP}{∠ABC}$的值不变，②$\frac{∠QMC}{∠ABC}$的值不变；其中只有一个结论正确，请择一证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

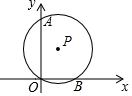    12．如图，在直角坐标系中，⊙P的圆心坐标为（1，$\sqrt{3}$），半径为2，⊙P分别交y轴，x轴于点A，B，求证：
    （1）AB是⊙P的直径；
    （2）直线y=$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$与⊙P相切于点A．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

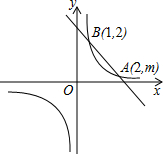    19．直线y1=k1x+b与双曲线y2=$\frac{{k}_{2}}{x}$相交于A（2，m），B（1，2）两点．
    （1）求直线和双曲线的解析式；
    （2）直接写出y1＞y2时自变量x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图，△ABC中，AD=8，AC=10，DC=6，AB=17，则BC的长是21．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．《九章算术》中记载：“今有竹高一丈，未折抵地，去根三尺，问折者高几何？”译文：有一根竹子原高一丈（1丈=10尺），中部有一处折断，竹梢触地面处离竹根3尺，试问折断处离地面多高？我们用线段OA和线段AB来表示竹子，其中线段AB表示竹子折断部分，用线段OB表示竹梢触地处离竹根的距离，则竹子折断处离地面的高度OA是4.55尺．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图1，Rt△ABC中，∠BAC=90°，AB=AC，∠ABC的平分线交直线AC于D，过点C作CE⊥BD，交直线BD于E．
    （1）请探究线段BD与CE的数量关系．
    （2）在（1）中，如果把BD改为∠ABC的外角∠ABF的平分线，其他条件均不变（如图2），（1）中的结论还成立吗？若成立，请写出证明过程；若不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．一个圆筒底面直径为10cm，高24cm，则桶内所能容下的最长木棒为26cm．

    查看答案和解析>>

    同步练习册答案