
【题目】山西省每年的体育考试分成必考科目与选考科目两部分.其中选考科目是从一分钟跳绳、掷实心球、坐位体前屈、仰卧起坐四个项目中选取一项.王红与李丽是一对好朋友且都在2020年参加中考,实心球是她俩的弱项,其他三项都非常强,体育考试选考的四个项目中,她俩一定不会选实心球.
(1)王红在选考项目中,选中坐位体前屈的概率是 .
(2)王红与李丽选取同一个选考项目的概率是多少? (在画树状图或列表时,“一分钟跳绳"用“![]() ”表示,“坐位体前屈”用“
”表示,“坐位体前屈”用“![]() "表示,“仰卧起坐”用“
"表示,“仰卧起坐”用“![]() ”表示,“掷实心球”用“
”表示,“掷实心球”用“![]() ”表示)
”表示)
(3)通过对我省某市2020年参加中考的学生进行随机调查,发现该市选择“坐位体前屈”的学生的频率稳定在![]() 左右,已知该市有
左右,已知该市有![]() 人参加2020年中考体育,请由此估计该市这
人参加2020年中考体育,请由此估计该市这![]() 名学生中选择“坐位体前屈”的人数.
名学生中选择“坐位体前屈”的人数.

科目:初中数学 来源: 题型:
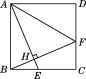
【题目】如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作BH⊥AE,垂足为点H,延长BH交CD于点F,连接AF.
(1)求证AE=BF;
(2)若正方形的边长是5,BE=2,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,其中∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.对于下列结论:①△CAM∽△DEM;②CD=2BE;③MPMD=MAME;④2CB2=CPCM.其中正确的是( )
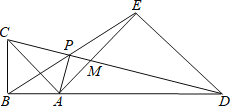
A. ①②B. ①②③C. ①②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
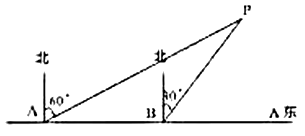
【题目】为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在![]() 处测得灯塔
处测得灯塔![]() 在北偏东
在北偏东![]() 方向上,继续航行1小时到达
方向上,继续航行1小时到达![]() 处,此时测得灯塔
处,此时测得灯塔![]() 在北偏东
在北偏东![]() 方向上.
方向上.
(1)求![]() 的度数;
的度数;
(2)已知在灯塔![]() 的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明准备进行如下操作实验:把一根长为![]() 的铁丝剪成两段,并把每一段围成一个正方形.
的铁丝剪成两段,并把每一段围成一个正方形.
(1)要使这两个正方形的面积之和等于![]() ,小明该怎么剪?
,小明该怎么剪?
(2)小刚对小明说:“这两个正方形的面积之和不可能等于![]() .”小刚的说法对吗?请说明理由.
.”小刚的说法对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
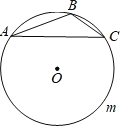
【题目】如图,△ABC中,∠ABC=120°,AC=2,⊙O是△ABC的外接圆,D是![]() 上任意一点(不包括点A、C),顺次连接四边形ABCD四边中点得到四边形EFGH,则四边形EFGH的周长的最大值为____________.
上任意一点(不包括点A、C),顺次连接四边形ABCD四边中点得到四边形EFGH,则四边形EFGH的周长的最大值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
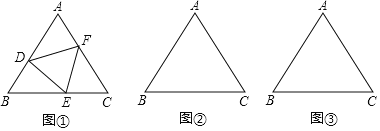
【题目】(概念提出)如图 ①,若正△DEF的三个顶点分别在正△ABC的边AB、BC、AC上,则我们称△DEF是正△ABC的内接正三角形.
(1)求证:△ADF≌△BED.
(问题解决)利用直尺和圆规作正三角形的内接正三角形(保留作图痕迹,不写作法).
(2)如图 ②,正△ABC的边长为a,作正△ABC的内接正△DEF,使△DEF的边长最短,并说明理由;
(3)如图③,作正△ABC的内接正△DEF,使FD⊥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
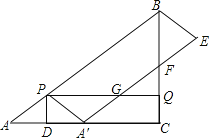
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8cm,AB=10cm.点P从点A出发,以5cm/s的速度从点A运动到终点B;同时,点Q从点C出发,以3cm/s的速度从点C运动到终点B,连结PQ;过点P作PD⊥AC交AC于点D,将△APD沿PD翻折得到△A′PD,以A′P和PB为邻边作A′PBE,A′E交射线BC于点F,交射线PQ于点G.设A′PBE与四边形PDCQ重叠部分图形的面积为Scm2,点P的运动时间为ts.
(1)当t为何值时,点A′与点C重合;
(2)用含t的代数式表示QF的长;
(3)求S与t的函数关系式;
(4)请直接写出当射线PQ将A′PBE分成的两部分图形的面积之比是1:3时t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com