
【题目】定义:两边的平方和与这两边乘积的差等于第三边平方的三角形叫做“和谐三角形”.如图1在![]() 中,若
中,若![]() ,则
,则![]() 是“和谐三角形”.
是“和谐三角形”.

(1)等边三角形一定是“和谐三角形”,是______命题(填“真”或“假”).
(2)若![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() ,若
,若![]() 是“和谐三角形”,求
是“和谐三角形”,求![]() .
.
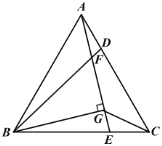
(3)如图2,在等边三角形![]() 的边
的边![]() ,
,![]() 上各取一点
上各取一点![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 的高,若
的高,若![]() 是“和谐三角形”,且
是“和谐三角形”,且![]() .
.

①求证:![]() .
.
②连结![]() ,若
,若![]() ,那么线段
,那么线段![]() ,
,![]() ,
,![]() 能否组成一个“和谐三角形”?若能,请给出证明:若不能,请说明理由.
能否组成一个“和谐三角形”?若能,请给出证明:若不能,请说明理由.
【答案】(1)真;(2)![]() .(3)能,证明见解析
.(3)能,证明见解析
【解析】
(1)利用“和谐三角形”的定义验证即可;
(2)若![]() 是“和谐三角形”,分
是“和谐三角形”,分![]() ,
,![]() ,
,![]() 三种情况,分别进行讨论即可;
三种情况,分别进行讨论即可;
(3)①先利用![]() 是“和谐三角形”和第(2)问的结论得出
是“和谐三角形”和第(2)问的结论得出![]() ,然后再利用等边三角形的性质证明
,然后再利用等边三角形的性质证明![]() ,则结论可证;
,则结论可证;
②先证明![]() ,得出
,得出![]() ,设出
,设出![]() ,
,![]() ,然后分别表示出
,然后分别表示出![]() ,然后用“和谐三角形”定义验证即可.
,然后用“和谐三角形”定义验证即可.
(1)设等边三角形三边分别为a,b,c
∵三角形为等边三角形
∴a=b=c
∵![]()
∴等边三角形是“和谐三角形”
故答案为“真”
(2)∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
①若![]() ,则
,则![]() .(舍去)
.(舍去)
②若![]() ,则
,则![]() ,
,
∴![]() ,得
,得![]() .
.
由勾股定理得![]()
∴![]() .
.
③若![]() ,则
,则![]() ,
,
∴![]() ,得
,得![]() .
.
由勾股定理得![]()
∴![]()
∵![]()
∴![]() (舍去)
(舍去)
综上可知,![]() 是“和谐三角形”时
是“和谐三角形”时![]() .
.
(3)①∵在等边三角形![]() 中,
中,
∴![]() ,
,![]() .
.
又∵![]() 是
是![]() 的高,
的高,![]() 是“和谐三角形”,
是“和谐三角形”,
∴![]() .
.
∴![]() .
.
∴![]() .
.
又∵![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
②
∵![]() ,
,![]()
∴![]() .
.
∴![]()
∴![]() .
.
由![]() ,
,![]() 知
知![]() ,
,
设![]() ,
,![]() ,则
,则![]() .
.
∴![]()
![]()
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴线段![]() ,
,![]() ,
,![]() 能组成一个和谐三角形.
能组成一个和谐三角形.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价![]() 元,乒乓球每盒定价
元,乒乓球每盒定价![]() 元,经洽谈后,甲店每买一-副球拍赠一盒乒乓球,乙店全部按定价的
元,经洽谈后,甲店每买一-副球拍赠一盒乒乓球,乙店全部按定价的![]() 折优惠.该班需买球拍
折优惠.该班需买球拍![]() 副,乒乓球若干盒(不小于
副,乒乓球若干盒(不小于![]() 盒).
盒).
(1)当购买乒乓球多少盒时,在两店购买付款一样?
(2)如果给你![]() 元,让你选择- -家商店去办这件事,你打算去哪家商店购买?为什么?
元,让你选择- -家商店去办这件事,你打算去哪家商店购买?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点![]() 、点
、点![]() 表示的数分别为
表示的数分别为![]() 、
、![]() ,则
,则![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ,线段
,线段![]() 的中点表示的数为
的中点表示的数为![]() .
.
(问题情境)
如图,数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为8,点
表示的数为8,点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点
出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为
出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为![]() 秒(
秒(![]() ).
).
(综合运用)
(1)填空:
①![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ________,线段
________,线段![]() 的中点表示的数为__________.
的中点表示的数为__________.
②用含![]() 的代数式表示:
的代数式表示:![]() 秒后,点
秒后,点![]() 表示的数为____________;点
表示的数为____________;点![]() 表示的数为___________.
表示的数为___________.
③当![]() _________时,
_________时,![]() 、
、![]() 两点相遇,相遇点所表示的数为__________.
两点相遇,相遇点所表示的数为__________.
(2)当![]() 为何值时,
为何值时,![]() .
.
(3)若点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,点
的中点,点![]() 在运动过程中,线段
在运动过程中,线段![]() 的长度是否发生变化?若变化,请说明理由;若不变,请求出线段
的长度是否发生变化?若变化,请说明理由;若不变,请求出线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,长方形![]() 的三个顶点的坐标为
的三个顶点的坐标为![]() ,
,![]() ,
,![]() ,且
,且![]() 轴,点
轴,点![]() 是长方形内一点(不含边界).
是长方形内一点(不含边界).

(1)求![]() ,
,![]() 的取值范围.
的取值范围.
(2)若将点![]() 向左移动8个单位,再向上移动2个单位到点
向左移动8个单位,再向上移动2个单位到点![]() ,若点
,若点![]() 恰好与点
恰好与点![]() 关于
关于![]() 轴对称,求
轴对称,求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象
如图所示,根据图中提供的信息,有下列说法:
①两人相遇前,甲的速度小于乙的速度; ②出发后1小时,两人行程均为10km;
③出发后1.5小时,甲的行程比乙多3km; ④甲比乙先到达终点.
其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年2月,市城区公交车施行全程免费乘坐政策,标志着我市公共交通建设迈进了一个新的时代.下图为某一条东西方向直线上的公交线路,东起职教园区站,西至富士康站,途中共设![]() 个上下车站点,如图所示:
个上下车站点,如图所示:
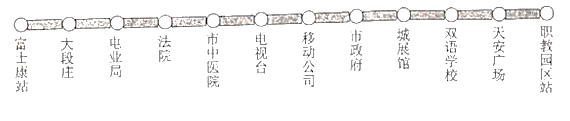
某天,小王从电业局站出发,始终在该线路的公交站点做志愿者服务,到![]() 站下车时,本次志愿者服务活动结束,如果规定向东为正,向西为负,当天的乘车站数按先后顺序依次记录如下(单位:站):
站下车时,本次志愿者服务活动结束,如果规定向东为正,向西为负,当天的乘车站数按先后顺序依次记录如下(单位:站): ![]() ;
;
![]() 请通过计算说明
请通过计算说明![]() 站是哪一站?
站是哪一站?
![]() 若相邻两站之间的平均距离为
若相邻两站之间的平均距离为![]() 千米,求这次小王志愿服务期间乘坐公交车行进的总路程是多少千米?
千米,求这次小王志愿服务期间乘坐公交车行进的总路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB=6cm,点D是线段AB上一动点,将线段CD绕点C逆时针旋转50°至CD′,连接BD′.设AD为xcm,BD′为ycm.
小夏根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
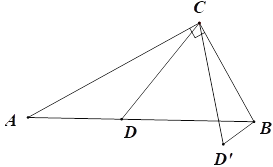
下面是小夏的探究过程,请补充完整.
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
| 1 | 2 | 3 | 3.5 | 4 | 5 | 6 |
| 3.5 | 1.5 | 0.5 | 0.2 | 0.6 | 1.5 | 2.5 |
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:当BD=BD'时,线段AD的长度约为_________![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com