
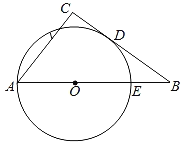
【题目】如图,BC是⊙O的切线,D是切点.连接BO并延长,交⊙O于点E、A,过A作AC⊥BC,垂足为C.若BD=8,BE=4,则AC=_____.
【答案】9.6
【解析】
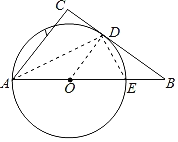
连接OD、AD、ED,根据切线的性质得到∠ODB=90°,根据圆周角定理得到∠ADE=90°,证明△BDE∽△BAD,根据相似三角形的性质求出AE,证明△BDO∽△BCA,求出AC.
连接OD、AD、ED,
∵BC是⊙O的切线,
∴∠ODB=90°,
∴∠ODE+∠BDE=90°,
∵AE为⊙O的直径,
∴∠ADE=90°,
∴∠DAE+∠AED=90°,
∵OD=OE
∴∠ODE=∠OED,
∴∠BDE=∠BAD,
∵∠B=∠B,
∴△BDE∽△BAD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,AE=12,
∵∠BDO=∠BCA,∠B=∠B,
∴△BDO∽△BCA,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,AC=9.6,
故答案为:9.6.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
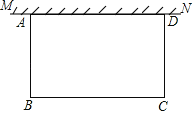
【题目】如图,在足够大的空地上有一段长为a(a≥50)米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
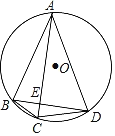
【题目】如图,四边形ABCD内接于⊙O,AC⊥BD于E.
(1)用尺规作图作DF⊥AB于F,交AC于G,并标出F、G(保留作图痕迹,不写作法);
(2)在(1)中,若∠BAD=45°,求证:EG=EC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,边长为2的等边△ABC是三棱镜的一个横截面.一束光线ME沿着与AB边垂直的方向射入到BC边上的点D处(点D与B,C不重合),反射光线沿DF的方向射出去,DK与BC垂直,且入射光线和反射光线使∠MDK=∠FDK.设BE的长为x,△DFC的面积为y,则下列图象中能大致表示y与x的函数关系的是( )
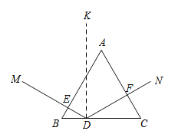
A. B.
B.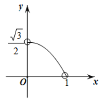 C.
C.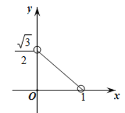 D.
D.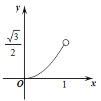
查看答案和解析>>
科目:初中数学 来源: 题型:
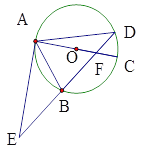
【题目】如图,已知⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB;
(1)求证:AE是⊙O的切线;
(2)已知点B是EF的中点,求证:△EAF∽△CBA
(3)已知AF=4,CF=2,在(2)的条件下,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别是
分别是![]() 的中点,连接
的中点,连接![]() .
.
(1)探索发现:
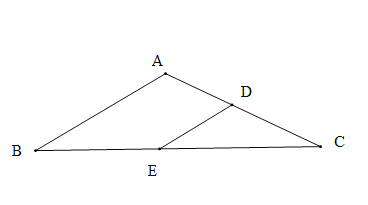
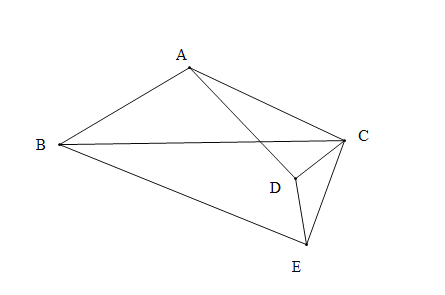
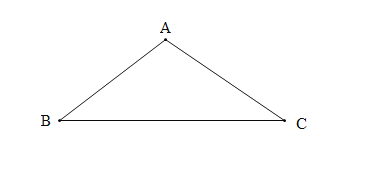
图1中,![]() 的值为_____________;
的值为_____________;![]() 的值为_________.
的值为_________.
(2)拓展探究
若将![]() 绕点
绕点![]() 逆时针方向旋转一周,在旋转过程中
逆时针方向旋转一周,在旋转过程中![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
当![]() 旋转至
旋转至![]() 三点在同一直线时,直接写出线段
三点在同一直线时,直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
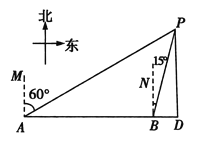
【题目】一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向,航行40海里到达B处,此时测得灯塔P在B的北偏东15°方向.
(1)求灯塔P到轮船航线的距离PD;(结果保留根号)
(2)当轮船从B处继续向东航行时,一艘快艇从灯塔P处同时前往D处,尽管快艇速度是轮船速度的2倍,但快艇还是比轮船晚15分钟到达D处,求轮船每小时航行多少海里.(结果精确到1海里,参考数据![]() ≈1.7)
≈1.7)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com