
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH= ![]() BD
BD
其中正确结论的为(请将所有正确的序号都填上).
【答案】①③④
【解析】解:∵△ACE是等边三角形,
∴∠EAC=60°,AE=AC,
∵∠BAC=30°,
∴∠FAE=∠ACB=90°,AB=2BC,
∵F为AB的中点,
∴AB=2AF,
∴BC=AF,
∴△ABC≌△EFA,
∴FE=AB,
∴∠AEF=∠BAC=30°,
∴EF⊥AC,故①正确,
∵EF⊥AC,∠ACB=90°,
∴HF∥BC,
∵F是AB的中点,
∴HF= ![]() BC,
BC,
∵BC= ![]() AB,AB=BD,
AB,AB=BD,
∴HF= ![]() BD,故④说法正确;
BD,故④说法正确;
∵AD=BD,BF=AF,
∴∠DFB=90°,∠BDF=30°,
∵∠FAE=∠BAC+∠CAE=90°,
∴∠DFB=∠EAF,
∵EF⊥AC,
∴∠AEF=30°,
∴∠BDF=∠AEF,
∴△DBF≌△EFA(AAS),
∴AE=DF,
∵FE=AB,
∴四边形ADFE为平行四边形,
∵AE≠EF,
∴四边形ADFE不是菱形;
故②说法不正确;
∴AG= ![]() AF,
AF,
∴AG= ![]() AB,
AB,
∵AD=AB,
则AD=4AG,故③说法正确,
所以答案是:①③④.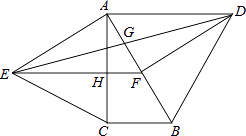
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°,以及对含30度角的直角三角形的理解,了解在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1 , 交x轴正半轴于点O2 , 以O2为圆心,O2O为半径画圆,交直线l于点P2 , 交x轴正半轴于点O3 , 以O3为圆心,O3O为半径画圆,交直线l于点P3 , 交x轴正半轴于点O4;…按此做法进行下去,其中 ![]() 的长为 .
的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至A处时,该岛位于正东方向的B处,为了防止某国海巡警干扰,就请求我国C处的渔监船前往B处护航,测得C与AB的距离CD为20海里,已知A位于C处的南偏西60°方向上,B位于C的南偏东45°的方向上,求A、B之间的距离.( ![]() ≈1.7,结果精确到1海里)
≈1.7,结果精确到1海里)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A在反比例函数y= ![]() (x<0)上,作Rt△ABC,点D为斜边AC的中点,连DB并延长交y轴于点E.若△BCE的面积为8,则k= .
(x<0)上,作Rt△ABC,点D为斜边AC的中点,连DB并延长交y轴于点E.若△BCE的面积为8,则k= . 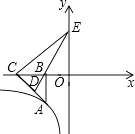
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣ ![]() ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).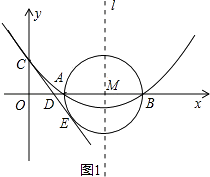
(1)求抛物线的解析式及A、B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;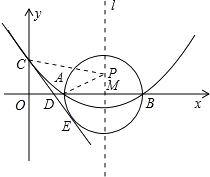
(3)以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF=60°,连接CF. 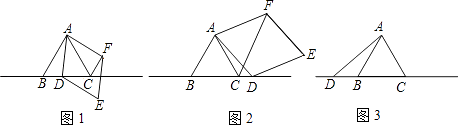
(1)如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;
(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;
(3)如图3,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元. ①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于B、C两点(点B在点C的左侧),与y轴交于点A,抛物线的顶点为D.
与x轴交于B、C两点(点B在点C的左侧),与y轴交于点A,抛物线的顶点为D.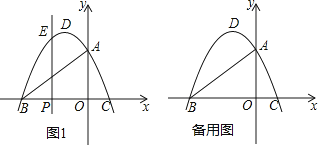
(1)填空:点A的坐标为( , ),点B的坐标为( , ),点C的坐标为( , ),点D的坐标为( , );
(2)点P是线段BC上的动点(点P不与点B、C重合)
①过点P作x轴的垂线交抛物线于点E,若PE=PC,求点E的坐标;
②在①的条件下,点F是坐标轴上的点,且点F到EA和ED的距离相等,请直接写出线段EF的长;
③若点Q是线段AB上的动点(点Q不与点A、B重合),点R是线段AC上的动点(点R不与点A、C重合),请直接写出△PQR周长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com