
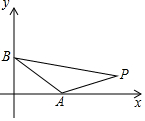
 如图,在平面直角坐标系中,点P(14,1),A(a,0),B(0,a),其中a>0,若△PAB的面积为18,求a的值.
如图,在平面直角坐标系中,点P(14,1),A(a,0),B(0,a),其中a>0,若△PAB的面积为18,求a的值. 分析 当0<a<14时,作PD⊥x轴于点D,由P(14,1),A(a,0),B(0,a)就可以表示出△ABP的面积,建立关于a的方程求出其解即可;
解答 解:当0<a<15时,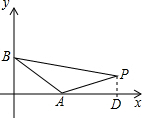
如图,作PD⊥x轴于点D,
∵P(14,1),A(a,0),B(0,a),
∴PD=1,OD=14,OA=a,OB=a,
∴S△PAB=S梯形OBPD-S△OAB-S△ADP=$\frac{1}{2}$×14(a+1)-$\frac{1}{2}$a2-$\frac{1}{2}$×1×(14-a)=18,
解得:a1=3,a2=12;
当a>15时,S△PAB=S△OAB-S梯形OBPD-S△ADP=18,
$\frac{1}{2}$a2-$\frac{1}{2}$×14×(1+a)-$\frac{1}{2}$×1×(a-14)=18,
解得a=$\frac{15+3\sqrt{41}}{2}$或$\frac{15-3\sqrt{41}}{2}$(舍弃)
故答案为:3或12或$\frac{15+3\sqrt{41}}{2}$.
点评 本题考查了坐标与图形的性质,三角形的面积公式的运用,梯形的面积公式的运用,点的坐标的运用,解答时运用三角形和梯形的面积建立方程求解是关键.


科目:初中数学 来源: 题型:解答题
 小明一家人春节期间参与了“支付宝集五福”活动,小明和姐姐都缺一个“敬业福”,恰巧爸爸有一个可以送给其中一个,两个人各设计了一个游戏,获胜者得到“敬业福”,请用适当的方法说明这两个游戏对小明和姐姐是否公平.
小明一家人春节期间参与了“支付宝集五福”活动,小明和姐姐都缺一个“敬业福”,恰巧爸爸有一个可以送给其中一个,两个人各设计了一个游戏,获胜者得到“敬业福”,请用适当的方法说明这两个游戏对小明和姐姐是否公平.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
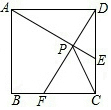 如图,在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在边DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,若AD=2,线段CP的最小值是( )
如图,在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在边DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,若AD=2,线段CP的最小值是( )| A. | $\sqrt{2}$ | B. | $\sqrt{5}$-1 | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
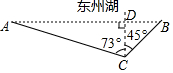 某市为了创建绿色生态城市,在城东建了“东州湖”景区,小明和小亮想测量“东州湖”东西两端A、B间的距离.于是,他们去了湖边,如图,在湖的南岸的水平地面上,选取了可直接到达点B的一点C,并测得BC=350米,点A位于点C的北偏西73°方向,点B位于点C的北偏东45°方向.
某市为了创建绿色生态城市,在城东建了“东州湖”景区,小明和小亮想测量“东州湖”东西两端A、B间的距离.于是,他们去了湖边,如图,在湖的南岸的水平地面上,选取了可直接到达点B的一点C,并测得BC=350米,点A位于点C的北偏西73°方向,点B位于点C的北偏东45°方向.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com