【题目】（7分）某产品每件的成本10元，试销阶段每件产品的销售价
（元）与产品的日销售量
（件）之间的关系如下表：
| 15 | 20 | 30 | … |
| 25 | 20 | 10 | … |
且日销售量（件）是销售价
（元）的一次函数.
(1)求出日销售量（件）与销售价（元）的函数关系式；
(2)要使每日的销售利润最大，每件产品的销售价应定为多少元？此时最大销售利润是多少？
【答案】（1）
；（2）
，所以当定价为25元时，利润w最大为225元.
【解析】
试题分析：（1）根据日销售量
（件）是销售价
（元）的一次函数，设y=kx+b，代入两组y与x的实数对即可求得k和b的值；
（2）销售利润=一件利润×销售件数，一件利润=销售价-成本，日销售量y是销售价x的一次函数，所获利润W为二次函数，运用二次函数的性质，可求最大利润．
试题解析：解：（1）设此一次函数关系式为y=kx+b，
则
，解得：
，
故一次函数的关系式为y=-x+40．
（2）设所获利润为W元，
则W=（x-10）（40-x）=-x2+50x-400=-（x-25）2+225
所以产品的售价应定为25元，此时每日的最大销售利润为225元．
科目：初中数学 来源： 题型：
【题目】已知二次函数y＝x2－4x＋3.
(1)该函数与x轴的交点坐标 ；
(2)在平面直角坐标系中，用描点法画出该二次函数的图象；
x | … | 0 | 1 | 2 | 3 | 4 | … |
y | … | 3 | 0 | －1 | 0 | 3 | … |
(3)根据图象回答：
①当自变量x的取值范围满足什么条件时，y＜0?
②当0≤x＜3时，y的取值范围是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，二次函数y＝ax2＋bx＋c的图象与x轴交于A，B两点，其中点A(－1，0)，点C(0，5)，点D(1，8)都在抛物线上，已知M为抛物线的顶点．
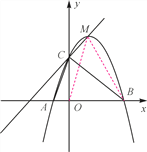
(1)求抛物线的表达式；
(2)求△MCB的面积；
(3)根据图形直接写出使直线MC表示的一次函数值大于二次函数值的x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】多项式x3－4x2y＋4xy2因式分解的结果是( )
A. x3－4xy(x－y) B. x(x－2y)2
C. x(4xy－4y2－x2) D. x(x2－4xy＋4y2)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知正方形ABCD的边长为6，E，F分别是AB、BC边上的点，且∠EDF=45°，将△DAE绕点D逆时针旋转90°，得到△DCM．
(1)求证：EF=MF；
(2)若AE=2，求FC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】PM2.5是大气中直径小于或等于0.0000025m的颗粒物，PM2.5粒径小，面积大，活性强，易附带有毒、有害物质（例如，重金属、微生物等），且在大气中的停留时间长、输送距离远，因而对人体健康和大气环境质量有较大的影响．在这里将数字0.0000025用科学计数法表示为（ ）
A. 0.25×10﹣5B. 0.25×10﹣6C. 2.5×10﹣5D. 2.5×10﹣6
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线y=﹣
x2+bx+4与x轴相交于A、B两点，与y轴相交于点C，若已知A点的坐标为A（﹣2，0）．
（1）求抛物线的解析式及它的对称轴；
（2）求点C的坐标，连接AC、BC并求线段BC所在直线的解析式；
（3）在抛物线的对称轴上是否存在点Q，使△ACQ为等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面给出四边形ABCD中，∠A、∠B、∠C、∠D的度数之比，其中能判定四边形ABCD为平行四边形的是( )
A. 1∶2∶3∶4 B. 2∶3∶2∶3
C. 2∶2∶3∶3 D. 1∶2∶2∶3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
