
如图①,在正方形ABCD中,点E、F分别为边BC、CD的中点,AF、DE相交于点G,可以证明①AF=DE ②AF⊥DE.
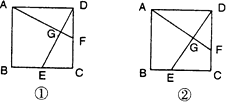
(1)如图②,若点E、F不是正方形ABCD的边BC、CD的中点,但满足CE=DF.则结论①AF=DE ②AF⊥DE是否仍然成立?(请直接回答“成立”或“不成立”,不必证明)
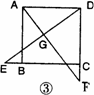
(2)如图③,若点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上,且CE=DF.则结论①AF=DE ②AF⊥DE是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;
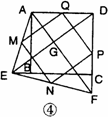
(3)如图④,在(2)的基础上,连接AE和EF,若点M、N、P、Q分别为AE、EF、FD、AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.
(1)结论①AF=DE,结论②AF⊥DE均成立(1分)
(2)结论①AF=DE,结论②AF⊥DE均成立(2分)
证明:∵四边形ABCD是正方形
∴∠ADF=∠DCE=90°,AD=DC(3分)
又∵DF=CE ∴△ADF≌△DCE
∴AF=DE,∠F=∠E(4分)
又∵∠E+∠EDC=90° ∴∠F+∠EDC=90°
∴∠DGF=90° ∴AF⊥DE(5分)
(3)四边形MNPQ是正方形(6分)
证明:∵AM=ME,AQ=QD ∴MQ//ED,![]() (7分)
(7分)
同理NP//ED,![]() ∴
∴![]()
∴四边形MNPQ是平行四边形(8分)
∵ME=MA,NE=NF ∴MN//AF,![]()
又∵AF=ED ∴MQ=MN ∴![]() MNPQ是菱形(9分)
MNPQ是菱形(9分)
∵AF⊥DE,MQ//ED ∴AF⊥MQ
又∵MN//AF ∴MN⊥MQ
∴∠QMN=90° ∴菱形MNPQ是正方形(10分)


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
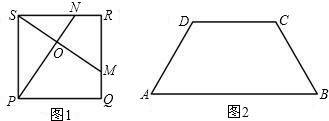 构造一个与上述命题类似的正确命题并加以证明.
构造一个与上述命题类似的正确命题并加以证明.查看答案和解析>>
科目:初中数学 来源: 题型:
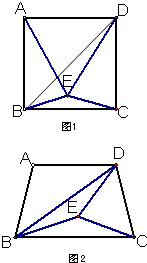 26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.
26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.查看答案和解析>>
科目:初中数学 来源: 题型:
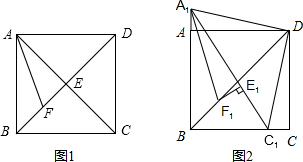 如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.
如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com