
【题目】如图,A、B、C、D、E、F是⊙O的六等分点. 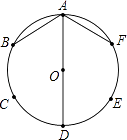
(1)连接AB、AD、AF,求证:AB+AF=AD;
(2)若P是圆周上异于已知六等分点的动点,连接PB、PD、PF,写出这三条线段长度的数量关系(不必说明理由).
【答案】
(1)解:解:连接OB、OF.
∵A、B、C、D、E、F是⊙O的六等分点,
∴AD是⊙O的直径,
且∠AOB=∠AOF=60°,
∴△AOB、△AOF是等边三角形.
∴AB=AF=AO=OD,
∴AB+AF=AD.
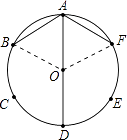
(2)当P在 ![]() 上时,PB+PF=PD;
上时,PB+PF=PD;
当P在 ![]() 上时,PB+PD=PF;
上时,PB+PD=PF;
当P在 ![]() 上时,PD+PF=PB
上时,PD+PF=PB
【解析】(1)连接OB、OF,得到等边△AOB、△AOF,据此并结合弦的性质,即可推理出AB=AF=AO=OD,从而得到AB+AF=AD;(2)由于AD是⊙O的直径,A、B、C、D、E、F是⊙O的六等分点,故点B与点F,点C与点E均关于AD对称,故分点P在不同的位置﹣﹣﹣在 ![]() 上、在
上、在 ![]() 上、在
上、在 ![]() 上三种情况讨论.
上三种情况讨论.
【考点精析】本题主要考查了圆心角、弧、弦的关系的相关知识点,需要掌握在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】按要求解答下列各题:
(1)解不等式:3x-5<2(2+3x);
(2)解不等式:2x-3≤![]() (x+2);
(x+2);
(3)解不等式: ![]() <x-1,并将解集在数轴上表示出来.
<x-1,并将解集在数轴上表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB。
![]()
(1)用尺规作图的方法作出线段AB的垂直平分线l(保留作图痕迹,不要求写出作法);
(2)在(1)中所作的直线l上任意取两点M、N(线段AB的上方),连接AM、AN。BM、BN。
求证:∠MAN=∠MBN。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于P(x,y)作变换得到P′(﹣y+1,x+1),例如:A1(3,1)作上述变换得到A2(0,4),再将A2做上述变换得到A3___________,这样依次得到A1,A2,A3,…An;…,则A2018的坐标为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
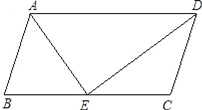
【题目】如图,已知平行四边形ABCD,DE是∠ADC的角平分线,交BC于点E.
(1)求证:CD=CE;
(2)若BE=CE,∠B=80°,求∠DAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
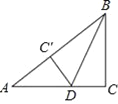
【题目】如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(1)计算:3( ![]() ﹣π)0﹣
﹣π)0﹣ ![]() +(﹣1)2011
+(﹣1)2011
(2)先化简,再求值: ![]() ,其中x=
,其中x= ![]() -3.
-3.
(3)如图,平行四边形ABCD的对角线AC、BD交于点O,E、F在AC上,G、H在BD上,且AF=CE,BH=DG. 求证:GF∥HE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A为x轴负半轴上一点,点B为x轴正半轴上一点,C(0,a),D(b,a),其中a,b满足关系式:|a+3|+(b-a+1)2=0.
(1)a=___,b=___,△BCD的面积为______;
(2)如图2,若AC⊥BC,点P线段OC上一点,连接BP,延长BP交AC于点Q,当∠CPQ=∠CQP时,求证:BP平分∠ABC;
(3)如图3,若AC⊥BC,点E是点A与点B之间一动点,连接CE,CB始终平分∠ECF,当点E在点A与点B之间运动时,![]() 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com