
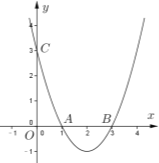
【题目】(1)已知二次函数![]() 的图像如图,请根据图像直接写出该二次函数图像经过怎样的左右平移,新图像通过坐标原点?
的图像如图,请根据图像直接写出该二次函数图像经过怎样的左右平移,新图像通过坐标原点?
(2)在关于二次函数图像的研究中,秦篆晔同学发现抛物线![]() (
(![]() )和抛物线
)和抛物线![]() (
(![]() )关于
)关于![]() 轴对称,基于协作共享,秦同学将其发现口诀化“
轴对称,基于协作共享,秦同学将其发现口诀化“![]() 、
、![]() 不变,
不变,![]() 相反”供大家分享,而在旁边补笔记的胡庄韵同学听成了“
相反”供大家分享,而在旁边补笔记的胡庄韵同学听成了“![]() 、
、![]() 相反,
相反,![]() 不变”,并按此法误写,然而按此误写的抛物线恰巧与原抛物线也对称,请你写出小胡同学所写的与原抛物线
不变”,并按此法误写,然而按此误写的抛物线恰巧与原抛物线也对称,请你写出小胡同学所写的与原抛物线![]() 的对称图形的解析式,并研究其与原抛物线的具体对称情况;
的对称图形的解析式,并研究其与原抛物线的具体对称情况;
(3)抛物线![]() 与
与![]() 轴从左到右交于
轴从左到右交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() 是其对称轴上一点,点
是其对称轴上一点,点![]() 在
在![]() 轴上,当点
轴上,当点![]() 满足怎样的条件,以点
满足怎样的条件,以点![]() 、
、![]() 、
、![]() 为顶点的三角形与△
为顶点的三角形与△![]() 有可能相似,请写出所有满足条件的点
有可能相似,请写出所有满足条件的点![]() 的坐标;
的坐标;
(4)![]() 、
、![]() 为抛物线
为抛物线![]() 上两点,且
上两点,且![]() 、
、![]() 关于
关于![]() 对称,请直接写出
对称,请直接写出![]() 、
、![]() 两点的坐标;
两点的坐标;
【答案】(1)向左移1个单位;(2)原抛物线关于原点对称;(3)![]() (4)
(4)![]()
【解析】
试题分析:(1)首先求得抛物线与x轴的交点,即可求得平移的方向和距离;
(2)根据“a、c相反,b不变”,即可求得对应的函数解析式,然后确定顶点即可判断;
(3)△MAB中M是在抛物线的对称轴上,则△MAB为等腰三角形,则△NBC是等腰三角形,同时根据∠OBC=45°,即已知等腰△NBC的一个角的度数,据此即可讨论,求解;
(4)设E的坐标是(![]() ,
,![]() ),由点E与F关于点D(
),由点E与F关于点D( ![]() ,0)对称,则可得F的坐标,然后根据点E和点F的纵坐标互为相反数即可列方程求解.
,0)对称,则可得F的坐标,然后根据点E和点F的纵坐标互为相反数即可列方程求解.
(1)y=(x-1)(x-3)与x轴的交点坐标为(1,0),(3,0),抛物线向左平移一个单位或者3个单位即可使新图像通过坐标原点。
(2)y=(x-1)(x-3)=![]() ,
,
因为小胡同学听成了a、c相反,b不变,
所以y=![]() ,
,
顶点坐标为(-2,1)
故与原抛物线关于原点对称。
(3)![]() 中M点是在抛物线的对称轴上,所以MA=MB,即
中M点是在抛物线的对称轴上,所以MA=MB,即![]() 为等腰三角形,
为等腰三角形,
又![]() 与
与![]() 相似,
相似,
![]() 为等腰三角形,
为等腰三角形,
![]() 在x轴上,
在x轴上,
![]() 或
或![]()
当![]() 时,即N点在B点右侧且BC=BN,易得
时,即N点在B点右侧且BC=BN,易得![]()
当![]() 时,即N点在B点左侧,
时,即N点在B点左侧,
若![]() 的底角为
的底角为![]() ,此时三角形为等腰三角形,易得N(0,0)或N(-3,0);
,此时三角形为等腰三角形,易得N(0,0)或N(-3,0);
若![]() 的顶角为
的顶角为![]() ,在
,在![]() 中BC=BN=
中BC=BN=![]() 易得
易得![]()
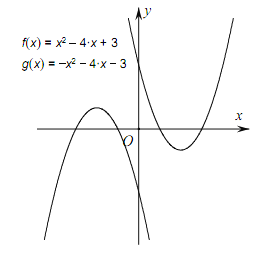
设E![]() ,
,
由点E与点F关于点D![]() 对称,则可得F
对称,则可得F![]() ,
,
所以点E和点F的纵坐标是互为相反数,既有![]()
解得![]() (舍)
(舍)
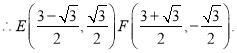


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】我市开展“美丽自贡,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:

(1)将条形统计图补充完整;
(2)扇形图中的“1.5小时”部分圆心角是多少度?
(3)求抽查的学生劳动时间的众数、中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式由等号左边变到右边变错的有( )
①a﹣(b﹣c)=a﹣b﹣c
②(x2+y)﹣2(x﹣y2)=x2+y﹣2x+y2
③﹣(a+b)﹣(﹣x+y)=﹣a+b+x﹣y
④﹣3(x﹣y)+(a﹣b)=﹣3x﹣3y+a﹣b.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明设计了一个魔术盒,当任意实数对(a,b)进入其中,会得到一个新的实数a2-2b+3,若将实数对(x,-2x)放入其中,得到一个新数为8,则x=___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是⊙O的直径.
(1)如图1,垂直于AD的两条弦B1C1,B2C2把圆周4等分,则∠B1的度数是 ,∠B2的度数是 ;
(2)如图2,垂直于AD的三条弦B1C1,B2C2,B3C3把圆周6等分,则∠B3的度数是 ;
(3)如图3,垂直于AD的n条弦B1C1,B2C2,B3 C3,…,BnCn把圆周2n等分,则∠Bn的度数是 (用含n的代数式表示∠Bn的度数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鄂州市化工材料经销公司购进一种化工原料若干千克,价格为每千克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100.在销售过程中,每天还要支付其他费用450元.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式.
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com