
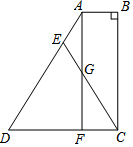
 如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且AB=FC,E为AD上一点,EC交AF于点G,EA=EG.
如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且AB=FC,E为AD上一点,EC交AF于点G,EA=EG.分析 先证明四边形ABCF是平行四边形.再证出四边形ABCF是矩形.得出∠AFC=90°,得出∠D=90°-∠DAF,∠ECD=90°-∠CGF.由等腰三角形的性质得出∠EAG=∠EGA.由对顶角相等得出∠DAF=∠CGF.证出∠D=∠ECD.即可得出结论.
解答 证明:∵AB∥DC,FC=AB,
∴四边形ABCF是平行四边形.
∵∠B=90°,
∴四边形ABCF是矩形.
∴∠AFC=90°,
∴∠D=90°-∠DAF,∠ECD=90°-∠CGF.
∵EA=EG,
∴∠EAG=∠EGA.
∵∠EGA=∠CGF,
∴∠DAF=∠CGF.
∴∠D=∠ECD.
∴ED=EC.
点评 本题考查了矩形的判定与性质、等腰三角形的判定与性质、直角三角形的性质、对顶角相等的性质;熟练掌握矩形的判定与性质是解决问题的关键.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
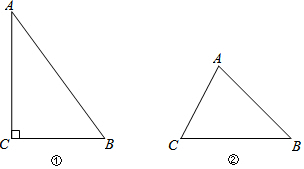
 如图,在直角梯形ABCD中,∠B=90°,AD∥BC,AB=8cm,AD=24cm,BC=26cm,点P从A出发,以每秒1cm的速度向点D运动;点Q从点C同时出发,以每秒3cm的速度向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动.设运动的时间为t秒.
如图,在直角梯形ABCD中,∠B=90°,AD∥BC,AB=8cm,AD=24cm,BC=26cm,点P从A出发,以每秒1cm的速度向点D运动;点Q从点C同时出发,以每秒3cm的速度向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动.设运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
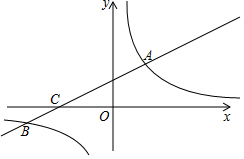 如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y=$\frac{6}{x}$相交于点A(m,3),B(-6,n),与x轴交于点C.
如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y=$\frac{6}{x}$相交于点A(m,3),B(-6,n),与x轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=mx2-4mx+2m-1(m≠0)与平行于x轴的一条直线交于A,B两点.
在平面直角坐标系xOy中,抛物线y=mx2-4mx+2m-1(m≠0)与平行于x轴的一条直线交于A,B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省枝江市九年级3月调研考试数学试卷(解析版) 题型:单选题
下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )(单位:cm.)
A. 3,4,8 B. 8,7,15
C. 5,5,11 D. 13,12,20
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com