Question

【题目】如图，已知的顶点A和AB边的中点C都在双曲线的一个分支上，点B在x轴上，则的面积为

A.3B.4C.6D.8

Answer 1

【答案】C

【解析】

,结合图形可得:S△ABO=S△AOM+S△AMB,分别求解出S△AOM、S△AMB的值，过点A、C分别作AM⊥OB于M、CD⊥OB于D,设点A坐标为(x,y),设B的坐标为(a,0),已知点C是线段AB的中点, 由点A位于反比例函数的图象上可得:xy=4,即S△AOM=2,接下来,根据点C的坐标为( ),同理可解得S△CDO的面积，接下来,由S△AMB=×AM×BM,MB=|ax|,AM=y,可解得S△AMB，即可确定△ABO的面积.

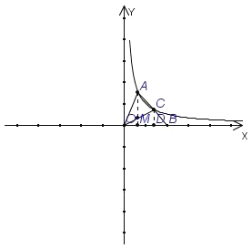
解:过点A、C分别作AM⊥OB于M、CD⊥OB于D,设点A坐标为(x,y)

∵ 顶点A在双曲线y=(x＞0)图象上

∴ xy=4

∵ AM⊥OB

∴ S△AMO=×AM×OM=×xy，S△AMB=×AM×BM (三角形的面积等于一边与此边上高的乘积的一半)

∵ S△AMO=×xy， xy=4

∴ S△AMO=2

设B的坐标为(a,0)

∵ 点C是线段AB的中点 点A、B坐标为(x,y)、(a,0)

∴ 点C坐标为()

∵ CD⊥OB 点C坐标为()

∴ S△CDO=×CD×OD=×()×()=2 (三角形的面积等于一边与此边上高的乘积的一半)

故ay=2

∵ S△AMB=×AM×BM，MB=|ax| ，AM=y

∴ S△AMB=span>×|ax|×y=4

∵ S△ABO=S△AOM+S△AMB，S△AOM=2，S△AMB=4

∴ S△ABO=6

即△ABO的面积是6,答案选C.