练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．分解因式
    （1）x2（a-b）-y2（a-b）
    （2）9（a+b）2-4（a-b）2．

    分析 （1）先提公因式a-b，再套用平方差公式分解；
    （2）先用平方差公式分解，再化简即可．

    解答 解：（1）原式=（a-b）（x2-y2）
    =（a-b）（x+y）（x-y）；
    （2）原式=[3（a+b）+2（a-b）][3（a+b）-2（a-b）]
    =（5a+b）（a+5b）．

    点评 本题考查了提公因式法，公式法分解因式．注意提取公因式后利用平方差公式进行二次分解，分解要彻底．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    6．解方程$\frac{x-1}{x}$-$\frac{2x}{x-1}$=3时，设$\frac{x-1}{x}$=y，则原方程可化为关于y的整式方程是（　　）
    A．y-$\frac{2}{y}$=3B．y2-2y=3C．y2-3y-2=0D．y2+3y-2=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．因式分解：
    （1）x（a-b）2+y（b-a）2
    （2）4x2-9．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

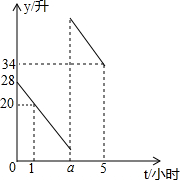    9．张师傅驾车从甲地去乙地，途中在加油站加了一次油，加油时，车载电脑显示还能行驶50千米．假设加油前、后汽车都以100千米/小时的速度匀速行驶，已知油箱中剩余油量y（升）与行驶时间t（小时）之间的关系如图所示．
    （1）求张师傅加油前油箱剩余油量y（升）与行驶时间t（小时）之间的关系式；
    （2）求出a的值；
    （3）求张师傅途中加油多少升？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．小东从甲地出发匀速前往相距20km的乙地，一段时间后，小明从乙地出发沿同一条路匀速前往甲地．小东出发2.5h后，在距乙地7.5km处与小明相遇，之后两人同时到达终点．图中线段AB、CD分别表示小东、小明与乙地的距离y（km）与小东所用时间x（h）的关系．
    （1）求线段AB、CD所表示的y与x之间的函数表达式；
    （2）小东出发多长时间后，两人相距16km？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．因式分解：
    （1）a5-a3
    （2）4-4（x-y）+（x-y）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

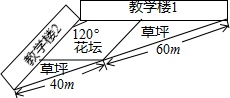    13．学校两幢教学楼之间有一块三角形地带，将其划分为三个区域：一块菱形和两块三角形．菱形作为花坛，两个三角形内铺上草皮，两幢教学楼的夹角为120°，其余尺寸如图所示，则菱形花坛的面积为$\frac{7200\sqrt{3}}{19}$m2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．分解因式：
    （1）2x2-18  （2）-3m+6m2-3m3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．模型介绍：古希腊有一个著名的“将军饮马问题”，大致内容如下：古希腊一位将军，每天都要巡查河岸侧 的两个军营A、B，他总是先去A营，再到河边饮马，之后再去B营，如图①，他时常想，怎么走才能使每天的路程之和最短呢？
    大数学家海伦曾用轴对称的方法巧妙的解决了这问题

    如图②，作B关于直线l的对称点B′，连接AB′与直线l交于点C，点C就是所求的位置．请你在下列的阅读、应用的过程中，完成解答．
    （1）理由：如图③，在直线L上任取一点C′，连结AC′，BC′，B′C′．
    ∵直线L是点B，B′的对称轴，点C，C′在L上．
    ∴CB=CB'，C′B=C'B'
    ∴AC+CB=AC+CB′=AB'．
    在△AC′B′中，∵AB′＜AC′+C′B′．
    ∴AC+CB＜AC′+C′B′．
    ∴AC+CB＜AC′+C′B′即AC+CB最小
    归纳小结：
    本问题实际是利用轴对称变换的思想，把A，B在直线的同侧问题转化为在直线的两侧，从而可利用“两 点之间线段最短”，即转化为“三角形两边之和大于第三边”的问题加以解决（其中C为AB′与l的交点，即A、C、B′三点共线）．
    本问题可拓展为“求定直线上一动点与直线外两定点的距离和的最小值”问题的数学模型．
    （2）模型应用
    如图④，正方形 ABCD 的边长为2，E为AB的中点，F是AC上一动点．
    求EF+FB的最小值
    分析：解决这个问题，可以借助上面的模型，由正方形的对称性可知，B与D关于直线AC对称，连结ED交AC于F，则EF+FB的最小值就是线段DE的长度，EF+FB的最小值是$\sqrt{5}$．

    如图⑤，已知⊙O的直径CD为4，∠AOD的度数为60°，点B是$\widehat{AD}$的中点，在直径CD上找一点P，使BP+AP的值最小，则BP+AP的最小值是2$\sqrt{2}$．
    如图⑥，一次函数y=-2x+4的图象与x、y轴分别交于点A，B两点，点O为坐标原点，点C与点D分别为线段OA、AB的中点，点P为OB上一动点．求PC+PD取得最小值时P点坐标．

    查看答案和解析>>

    同步练习册答案