
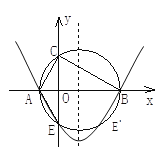
【题目】如图,在Rt△ABC中,∠ACB=90°,BC>AC,以斜边AB 所在直线为x轴,以斜边AB上的高所在直线为y轴,建立直角坐标系,若OA2+OB2= 17, 且线段OA、OB的长度是关于x的一元二次方程x2-mx+2(m-3)=0的两个根.
(1)求C点的坐标;
(2)以斜边AB为直径作圆与y轴交于另一点E,求过A、B、E 三点的抛物线的关系式,并画出此抛物线的草图.
(3)在抛物线上是否存在点P,使△ABP与△ABC全等?若存在,求出符合条件的P点的坐标;若不存在,说明理由.
【答案】(1)C(0,2);(2)y=![]() .(3)(0,-2)和(3,-2)
.(3)(0,-2)和(3,-2)
【解析】本题是二次函数与圆以及全等三角形相结合的题目,难度较大
(1)线段OA、OB的长度是关于x的一元二次方程x2-mx+2(m-3)=0的两个根.根据韦达定理就可以得到关于OA,OB的两个式子,再已知OA2+OB2=17,就可以得到一个关于m的方程,从而求出m的值.求出OA,OB.根据OC2=OAOB就可以求出C点的坐标;
(2)由第一问很容易求出A,B的坐标.连接AB的中点,设是M,与E,在直角△OME中,根据勾股定理就可以求出OE的长,得到E点的坐标,利用待定系数法就可以求出抛物线的解析式;
(3)E点就是满足条件的点.同时C,E关于抛物线的对称轴的对称点也是满足条件的点.
解:(1)线段OA,OB的长度是关于x的一元二次方程x2-mx+2(m-3)="0" 的两个根,
∴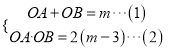
又∵OA2+OB2=17,∴(OA+OB)2-2·OA·OB=17.③
把①,②代入③,得m2-4(m-3) =17,∴m2-4m-5=0.解之,得m=-1或m=5.
又知OA+OB=m>0,∴m=-1应舍去.
∴当m=5时,得方程:x2-5x+4=0,解之,得x=1或x=4.
∵BC>AC,∴OB>OA,∴OA=1,OB=4,
在Rt△ABC中,∠ACB=90°,CO⊥AB,
∴OC2=OA·OB=1×4=4.∴OC=2,∴C(0,2)
(2)∵OA=1,OB=4,C,E两点关于x轴对称,
∴A(-1,0),B(4,0),E(0,-2).
设经过A,B,E三点的抛物线的关系式为
y=ax2+bx+c,则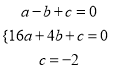 ,解之,得
,解之,得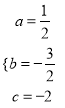
∴所求抛物线关系式为y=![]() .
.
(3)存在.∵点E是抛物线与圆的交点.
∴Rt△ACB≌Rt△AEB,∴E(0,-2)符合条件.
∵圆心的坐标(![]() ,0 )在抛物线的对称轴上.
,0 )在抛物线的对称轴上.
∴这个圆和这条抛物线均关于抛物线的对称轴对称.
∴点E关于抛物线对称轴的对称点E′也符合题意.
∴可求得E′(3,-2).
∴抛物线上存在点P符合题意,它们的坐标是(0,-2)和(3,-2)


科目:初中数学 来源: 题型:
【题目】某批发商计划将一批海产品由A地运往B地.汽车货运公司和铁路货运公司均开办海产品运输业务.已知运输路程为120千米,汽车和火车的速度分别为60千米/时、100千米/时.两货运公司的收费项目及收费标准如下表所示:
运输工具 | 运输费单价/ (元/吨·千米) | 冷藏费单价/ (元/吨·小时) | 过路费/元 | 装卸及管理费/元 |
汽 车 | 2 | 5 | 200 | 0 |
火 车 | 1.8 | 5 | 0 | 1600 |
注:“元/吨·千米”表示每吨货物每千米的运费;“元/吨·小时”表示每吨货物每小时的冷藏费.
(1)设该批发商待运的海产品有x(吨),汽车货运公司和铁路货运公司所要收取的费用分别为y1(元)和y2(元),试求y1、y2与x之间的函数关系式.
(2)若该批发商待运的海产品不少于30吨,为节省运费,他应选择哪个货运公司承担运输业务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm.
(1)观察图形填写下表:
链条节数(节) | 2 | 3 | 4 |
链条长度(cm) |
|
|
|
(2)如果x节链条的总长度是y,求y与x之间的关系式;
(3)如果一辆某种型号自行车的链条(安装前)由80节这样的链条组成,那么这根链条完成链接(安装到自行车上)后,总长度是多少cm?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
关于![]() ,
,![]() 的二元一次方程
的二元一次方程![]() 有一组整数解
有一组整数解![]() 则方程
则方程![]() 的全部整数解可表示为
的全部整数解可表示为![]() (
(![]() 为整数).
为整数).
问题:求方程![]() 的所有正整数解.
的所有正整数解.
小明参考阅读材料,解决该问题如下:
解:该方程一组整数解为![]() 则全部整数解可表示为
则全部整数解可表示为![]() (
(![]() 为整数).
为整数).
因为![]() 解得
解得![]() .因为
.因为![]() 为整数,所以
为整数,所以![]() 0或
0或![]() .
.
所以该方程的正整数解为![]() 和
和![]() .
.
请你参考小明的解题方法, 完成下面的问题:
(1)方程![]() 的全部正整数解为______________;
的全部正整数解为______________;
(2)方程![]() 的全部整数解表示为:
的全部整数解表示为: ![]() (
(![]() 为整数);
为整数);
(3)方程![]() 的正整数解有多少组? 请说明理由.
的正整数解有多少组? 请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师家买了一套新房,其结构如图所示(单位:m).他打算将卧室铺上木地板,其余部分铺上地砖.
(1)木地板和地砖分别需要多少平方米?
(2)如果地砖的价格为每平方米x元,木地板的价格为每平方米3x元,那么王老师需要花多少钱?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D、F、E、G都在△ABC的边上,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.(请在下面的空格处填写理由或数学式)
解:∵EF∥AD,(已知)
∴∠2= ( )
∵∠1=∠2,(已知)
∴∠1= ( )
∴ ∥ ,( )
∴∠AGD+ =180°,(两直线平行,同旁内角互补)
∵ ,(已知)
∴∠AGD= (等式性质)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线CD与EF相交于点O,∠COE=60°,将一直角三角尺AOB的直角顶点与O重合,OA平分∠COE.

(1)求∠BOD的度数;
(2)将三角尺AOB以每秒3°的速度绕点O顺时针旋转,同时直线EF也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(0≤t≤40).
①当t为何值时,直线EF平分∠AOB;
②若直线EF平分∠BOD,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:每购买500元商品,就能获得一次转动转盘的机会,如果转盘停止后,指针上对准500、200、100、50、10的区域,顾客就可以获得500元、200元、100元、50元、10元的购物券一张(转盘等分成20份)。

(1)小华购物450元,他获得购物券的概率是多少?
(2)小丽购物600元,那么:
① 她获得50元购物券的概率是多少?
② 她获得100元以上(包括100元)购物券的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一个直角坐标系中作出y=![]() x2,y=
x2,y=![]() x2-1的图象.
x2-1的图象.
(1)分别指出它们的开口方向、对称轴以及顶点坐标;
(2)抛物线y=![]() x2-1与抛物线y=
x2-1与抛物线y=![]() x2有什么关系?
x2有什么关系?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com