
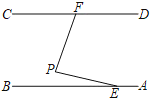
【题目】如图,在同一平面内,两条平行的高速公路AB和CD之间有一条“L”型道路连通,“L”型道路中的EP=FP=20千米,∠BEP=12°,∠EPF=80°,求AB和CD之间的距离.(参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】(1)计算:(![]() ﹣1)0+2sin30°-
﹣1)0+2sin30°-![]() +|﹣2017|;
+|﹣2017|;
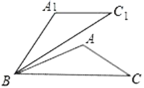
(2)如图,在△ABC中,已知∠ABC=30°,将△ABC绕点B逆时针旋转50°后得到△A1BC1,若∠A=100°,求证:A1C1∥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是某体育看台侧面的示意图,观众区AC的坡度i=1:2,顶端C离水平地面AB的高度为15m,顶棚外沿处的点E恰好在点A的正上方,从D处看E处的仰角α=30°,竖直的立杆上C,D两点间的距离为5m.
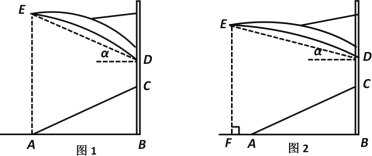
(1)求观众区的水平宽度AB.
(2)求图1中点E离水平地面的高度EA.
(3)因为遮阳需要,现将顶棚ED绕D点逆时针转动11°30′,若E点在地面上的铅直投影是点F(图2),求AF.(sin11°30′≈0.20,cos11°30′≈0.98,tan11°30′≈0.20;sin18°30′≈0.32,cos18°30′≈0.95,tan18°30′≈0.33,结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种商品,若将50件该商品按标价打八折销售,比按原标价销售这些商品少获利200元.
![]() 求该商品的标价为多少元;
求该商品的标价为多少元;
![]() 已知该商品的进价为每件12元,根据市场调査:若按
已知该商品的进价为每件12元,根据市场调査:若按![]() 中标价销售,该商场每天销售100件;每涨1元,每天要少卖5件
中标价销售,该商场每天销售100件;每涨1元,每天要少卖5件![]() 那么涨价后要使该商品每天的销售利润最大,应将销售价格定为每件多少元?最大利润是多少?
那么涨价后要使该商品每天的销售利润最大,应将销售价格定为每件多少元?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△EFG中,∠G=90°,![]() ,正方形ABCD的边长为1,将正方形ABCD和△EFG如图放置,AD与EF在一条直线上,点A与点E重合.现将正方形ABCD沿EF方向以每秒1个单位的速度匀速运动,当点A与点F重合时停止.在这个运动过程中,正方形ABCD和△EFG重叠部分的面积S与运动时间t的函数图象大致是( )
,正方形ABCD的边长为1,将正方形ABCD和△EFG如图放置,AD与EF在一条直线上,点A与点E重合.现将正方形ABCD沿EF方向以每秒1个单位的速度匀速运动,当点A与点F重合时停止.在这个运动过程中,正方形ABCD和△EFG重叠部分的面积S与运动时间t的函数图象大致是( )
A.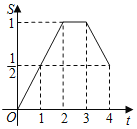 B.
B.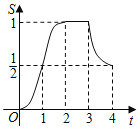
C.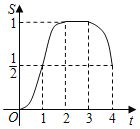 D.
D.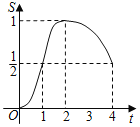
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②2a+b=0;③3a+c>0;④4a﹣2b+c<0:⑤9a+3b+c<0.其中结论正确的个数有( )
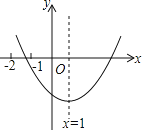
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(学习心得)
于彤同学在学习完“圆”这一章内容后,感觉到一些几何问题如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.
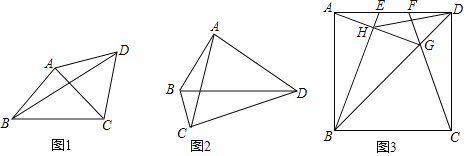
例如:如图1,在△ABC中,AB=AC,∠BAC=90°,D是△ABC外一点,且AD=AC,求∠BDC的度数.若以点A为圆心,AB为半径作辅助⊙A,则点C、D必在⊙A上,∠BAC是⊙A的圆心角,而∠BDC是圆周角,从而可容易得到∠BDC= °.
(2)(问题解决)
如图2,在四边形ABCD中,∠BAD=∠BCD=90°,∠BDC=25°,求∠BAC的度数.
(3)(问题拓展)
如图3,如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
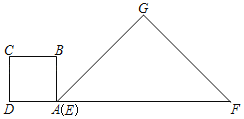
【题目】为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度![]() ,他站在距离教学楼底部
,他站在距离教学楼底部![]() 处6米远的地面
处6米远的地面![]() 处,测得宣传牌的底部
处,测得宣传牌的底部![]() 的仰角为
的仰角为![]() ,同时测得教学楼窗户
,同时测得教学楼窗户![]() 处的仰角为
处的仰角为![]() (
(![]() 、
、![]() 、
、![]() 、
、![]() 在同一直线上).然后,小明沿坡度
在同一直线上).然后,小明沿坡度![]() 的斜坡从
的斜坡从![]() 走到
走到![]() 处,此时
处,此时![]() 正好与地面
正好与地面![]() 平行.
平行.
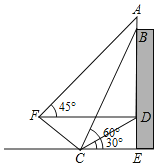
(1)求点![]() 到直线
到直线![]() 的距离(结果保留根号);
的距离(结果保留根号);
(2)若小明在![]() 处又测得宣传牌顶部
处又测得宣传牌顶部![]() 的仰角为
的仰角为![]() ,求宣传牌的高度
,求宣传牌的高度![]() (结果精确到0.1米,
(结果精确到0.1米,![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接“5.1”小长假的购物高峰,大冶雨润某运动品牌服装店准备购进甲、乙两种服装,已知每件甲服装进价比每件乙服装进价多20元,售价在进价的基础上加价50%,通过初步预算,若以4800元购进的甲服装比以4200元购进乙服装的件数少10件.
(1)求甲、乙两种服装的销售单价.
(2)现老板计划购进两种服装共100件,其中甲种服装不少于65件,若购进这100件服装的费用不超过7500元,则甲种服装最多购进多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com