
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:选择题
| A. | 如果a2=b2,那么|a|=|b| | B. | 内错角相等 | ||
| C. | 周长相等的两个三角形全等 | D. | 若a>b,则ac2>bc2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
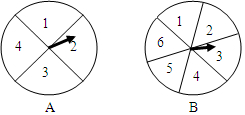 如图,有两个可以自由转动的转盘A、B,转盘A被均匀分成4等份,每份标上数字1、2、3、4四个数字;转盘B被均匀地分成6等份,每份分别标上1,2,3,4,5,6六个数字.有人为甲乙两人设计了一个游戏,其规则如下:
如图,有两个可以自由转动的转盘A、B,转盘A被均匀分成4等份,每份标上数字1、2、3、4四个数字;转盘B被均匀地分成6等份,每份分别标上1,2,3,4,5,6六个数字.有人为甲乙两人设计了一个游戏,其规则如下:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
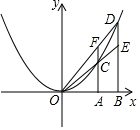 如图,在x轴上有两点A(m,0),B(n,0)(n>m>0),分别过点A,点B作x轴的垂线,交抛物线y=x2于点C,点D.直线OC交直线BD于点E,直线OD交直线AC于点F,点E,点F的纵坐标分别记作yE,yF
如图,在x轴上有两点A(m,0),B(n,0)(n>m>0),分别过点A,点B作x轴的垂线,交抛物线y=x2于点C,点D.直线OC交直线BD于点E,直线OD交直线AC于点F,点E,点F的纵坐标分别记作yE,yF查看答案和解析>>
科目:初中数学 来源: 题型:解答题
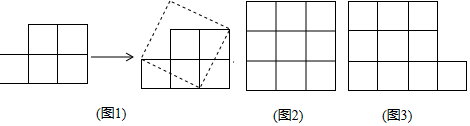
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在扇形OACB中,∠AOB=120°,⊙O′为弓形ACB的最大的内切圆,若AB的长为2π,则⊙O′的周长为( )
在扇形OACB中,∠AOB=120°,⊙O′为弓形ACB的最大的内切圆,若AB的长为2π,则⊙O′的周长为( )| A. | π | B. | $\frac{2}{3}$π | C. | $\frac{3}{2}$π | D. | 2π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com