
����Ŀ�����о�̩�ǹ�˾����![]() �����������ס������ֲ�Ʒ��ÿ��ÿ������
�����������ס������ֲ�Ʒ��ÿ��ÿ������![]() ���ײ�Ʒ��
���ײ�Ʒ��![]() ���Ҳ�Ʒ.�����г������ã��ײ�Ʒÿ���ɻ���
���Ҳ�Ʒ.�����г������ã��ײ�Ʒÿ���ɻ���![]() Ԫ���Ҳ�Ʒÿ���ɻ���
Ԫ���Ҳ�Ʒÿ���ɻ���![]() Ԫ.��ʵ�������У������Ҳ�Ʒ��Ҫ����֧��һ���ķ��ã��������㣬ÿ����
Ԫ.��ʵ�������У������Ҳ�Ʒ��Ҫ����֧��һ���ķ��ã��������㣬ÿ����![]() ���Ҳ�Ʒ������ÿ���Ҳ�Ʒƽ��ݶ������
���Ҳ�Ʒ������ÿ���Ҳ�Ʒƽ��ݶ������![]() Ԫ����ÿ�찲��
Ԫ����ÿ�찲��![]() �������Ҳ�Ʒ.
�������Ҳ�Ʒ.
(1)������Ϣ�����
��Ʒ���� | ÿ�칤����(��) | ÿ�����(��) | ÿ����Ʒ�ɻ�����(Ԫ) |
�� |
| ||
�� |
|
|
(2)��ÿ�������ײ�Ʒ�ɻ�õ�����������Ҳ�Ʒ�ɻ�õ������![]() Ԫ�����ʣ�����ҵÿ�������ס��Ҳ�Ʒ�ɻ���������Ƕ���Ԫ?
Ԫ�����ʣ�����ҵÿ�������ס��Ҳ�Ʒ�ɻ���������Ƕ���Ԫ?
���𰸡�(1) ![]() ��
��![]() ��
��![]() ��(2)����ҵÿ�������ס��Ҳ�Ʒ�ɻ����������
��(2)����ҵÿ�������ס��Ҳ�Ʒ�ɻ����������![]() Ԫ.
Ԫ.
��������
��1����ÿ�찲��x�������Ҳ�Ʒ����ÿ�찲�ţ�65-x���������ײ�Ʒ��ÿ�������x���Ҳ�Ʒ��ÿ��������Ϊ��120-2x��Ԫ��ÿ�������2��65-x�����ײ�Ʒ�����ʵý⣻
��2����������=ÿ����Ʒ�������������������ÿ�������ײ�Ʒ�ɻ�õ�����������Ҳ�Ʒ�ɻ�õ������650Ԫ�����ɵó�����x��һԪ���η��̣���֮ȡ���Сֵ���ɵó����ۣ�
�⣺��1����ÿ�찲��x�������Ҳ�Ʒ����ÿ�찲�ţ�65-x���������ײ�Ʒ��ÿ�������x���Ҳ�Ʒ��ÿ��������Ϊ��120-2x��Ԫ��ÿ�������2��65-x�����ײ�Ʒ��
�ʴ�Ϊ��![]() ��
��![]() ��
��![]() ��
��
��2�������⣬�ã�15��2��65-x��-��120-2x��x=650��
�������ã�x2-75x+650=0��
��ã�x1=10��x2=65���������⣬��ȥ����
��15��2��65-x��+��120-2x��x=2650��
�𣺸���ҵÿ�������ס��Ҳ�Ʒ�ɻ����������2650Ԫ��


 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д� ѧҵ����һ��һ��ϵ�д�
ѧҵ����һ��һ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���� ̽������
�� ![]() _________��
_________��
�� ![]() _________��
_________��
�� ![]() _________��
_________��
�� _________________��
�� ��
�� ��������
д����n����ʽ���ú�����ĸ![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
�� ������
�� ![]() _______��
_______��
�� ��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ 2 �������� ABCD �У��� P ��Q �ֱ��DZ� AB �� BC �ϵ��������㣨��� A ��B ��C ���غϣ���ʼ�ձ��� BP BQ, AQ QE ��QE �����������ƽ����CE �ڵ� E �� AE ��CD �ڵ� F ������ PQ ��
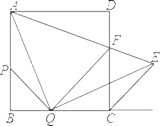
��1����֤�� APQ �� QCE ��
��2����QAE �Ķ�����
��3���� BQ x ���� x Ϊ��ֵʱ�� QF CE ���������ʱAQF �������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и����ֱ�������Ӧ�ļ�����
-2.5��-0.151515����0��8��![]() ��
��![]() ��
��![]() ��-0.5252252225����ÿ����5֮����������1��2��
��-0.5252252225����ÿ����5֮����������1��2��
��������___________________________________________________������
����������___________________________________________________������
��������___________________________________________________������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
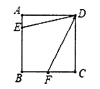
����Ŀ����ͼ��������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() ����
����![]() ��
��![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() ���е㣬��
���е㣬��![]() ����
����![]() �ij�Ϊ_______��
�ij�Ϊ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
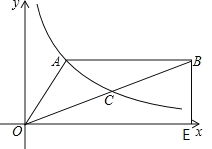
����Ŀ����ͼ��˫����y=![]() ��x��0��������OAB�Ķ���A��OB���е�C��AB��x�ᣬ��A������Ϊ��2��3����BE��x�ᣬ����ΪE��
��x��0��������OAB�Ķ���A��OB���е�C��AB��x�ᣬ��A������Ϊ��2��3����BE��x�ᣬ����ΪE��
��1��ȷ��k��ֵ��
��2������D��3��m����˫�����ϣ���ֱ��AD�Ľ���ʽ��
��3��������OAB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
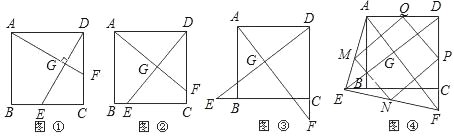
����Ŀ����ͼ1����������ABCD�У���E��F�ֱ�Ϊ��BC��CD���е㣬AF��DE�ཻ�ڵ�G����ɵý��ۣ���AF��DE����AF��DE������֤������
��1����ͼ��������E��F����������ABCD�ı�BC��CD���е㣬������CE��DF��������Ľ����������Ƿ���Ȼ����������ֱ�ӻش𡰳���������������
��2����ͼ��������E��F�ֱ���������ABCD�ı�CB���ӳ��ߺ�DC���ӳ����ϣ���CE��DF����ʱ����Ľ����������Ƿ���Ȼ����������������д��֤�����̣�������������˵�����ɣ�
��3����ͼ�����ڣ�2���Ļ����ϣ�����AE��EF������M��N��P��Q�ֱ�ΪAE��EF��FD��AD���е㣬�����ж��ı���MNPQ�ǡ����Ρ����Ρ������Ρ��������Ρ��е���һ�֣���д��֤�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��߳����ȵ��������������У�ÿ�������ζ���һ���������ں���y=x��ͼ���ϣ��������ҵ�3���������е�һ������A������Ϊ��8��4������Ӱ�����β��ֵ���������������μ�ΪS1��S2��S3������Sn����Sn��ֵΪ__�����ú�n�Ĵ���ʽ��ʾ��nΪ��������
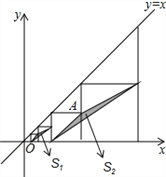
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0���IJ���ͼ����ͼ��ʾ��ͼ����㣨��1��0�����Գ���Ϊֱ��x=2�����н��ۣ���1��4a+b=0����2��9a+c����3b����3��7a��3b+2c��0����4������A����3��y1������B����![]() ��y2������C��7��y3���ڸú���ͼ���ϣ���y1��y3��y2����5��������a��x+1����x��5��=��3������Ϊx1��x2����x1��x2����x1����1��5��x2��������ȷ�Ľ����У�������
��y2������C��7��y3���ڸú���ͼ���ϣ���y1��y3��y2����5��������a��x+1����x��5��=��3������Ϊx1��x2����x1��x2����x1����1��5��x2��������ȷ�Ľ����У�������

A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com