
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -50% | B. | 0% | C. | 12.5% | D. | 15% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
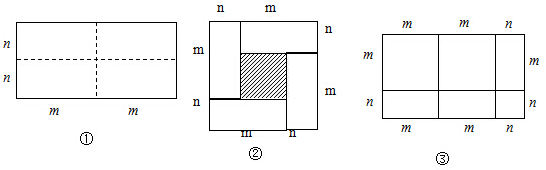
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,以点A为圆心处有一个半径为0.7km的圆形森林公园,在森林公园附近有B、C两个村庄,现要在B、C两村庄之间修一条长为2km的笔直公路,将两村连通.经测得,∠ABC=45°,∠ACB=30°,问此公路是否会穿过该森林公园.请通过计算说明理由.
如图,以点A为圆心处有一个半径为0.7km的圆形森林公园,在森林公园附近有B、C两个村庄,现要在B、C两村庄之间修一条长为2km的笔直公路,将两村连通.经测得,∠ABC=45°,∠ACB=30°,问此公路是否会穿过该森林公园.请通过计算说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com