
| 1 |
| 2 |
| 1 |
| 2 |
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源:三点一测丛书 八年级数学 下 (北京师大版课标本) 北京师大版课标本 题型:022
填写下面推理的理由:
已知:如图,AO∥CB,AD∥OB,求证:∠O+∠1=180°.
证明:∵AD∥OB(已知),
∴∠OBC=∠1( ).
∵AO∥CB(已知),
∴∠O+∠OBC=180°( )
∴∠O+∠1=180°( ).

查看答案和解析>>
科目:初中数学 来源:三点一测丛书 八年级数学 下 (北京师大版课标本) 北京师大版课标本 题型:022
填写下面推理的理由:
已知:如图,AB∥CD,求证:∠BED=∠B+∠D.
证明:过点E作EF∥AB.
∴∠BEF=∠B( ).
又∵AB∥CD(已知),
∴CD∥EF( ).
∴∠FED=∠D( ).
∴∠BEF+∠FED=∠B+∠D.
即∠BED=∠B+∠D.

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
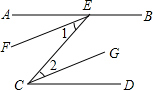
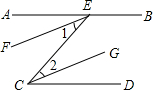
 ∠AEC (________)
∠AEC (________) ∠DCE,∴∠1=∠2
∠DCE,∴∠1=∠2查看答案和解析>>
科目:初中数学 来源: 题型:
填写证明的理由![]() 。
。
已知:如右图,AB∥CD,EF、CG分别是∠AEC、∠ECD的角平分线;求证:EF∥CG。
证明:∵ AB∥CD(已知)
∴ ∠AEC=∠DCE ( ![]() )
)
又 ∵ EF平分∠AEC (已知)
∴ ∠1= ![]() ∠ ( )
∠ ( )
同理 ∠2= ![]() ∠
∠ ![]() ∴ ∠1=∠2
∴ ∠1=∠2
∴ EF∥CG ( )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com