
 ,经过点(1,-3)、(3,-2),与x轴交于A、B两点,与y轴交于点C.D、E分别是边AC、BC上的两个动点(不与A、
,经过点(1,-3)、(3,-2),与x轴交于A、B两点,与y轴交于点C.D、E分别是边AC、BC上的两个动点(不与A、 B重合),且保持DE∥AB.以DE为边向上作正方形DEFG.
B重合),且保持DE∥AB.以DE为边向上作正方形DEFG. 解:(1)设二次函数解析式为y=a(x-
解:(1)设二次函数解析式为y=a(x- )2+k,
)2+k, ,k=-
,k=- ,
, (x-
(x- )2-
)2- ;
;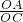 =
= =
= ,
,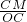 =
= ,
,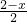 =
= ,
, ,
, ;
;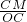 =
= ,
,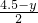 =
=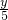 ,
,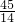 .
.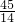 .
.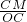 =
= 即可得出结论.
即可得出结论.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:解答题
 米的水管,水管顶端装有一个喷水头,已知喷出的抛物线形水柱在与池中心的水平距离为3米处达到最高高度为
米的水管,水管顶端装有一个喷水头,已知喷出的抛物线形水柱在与池中心的水平距离为3米处达到最高高度为 米,
米, ),水柱的最高点的坐标为(3,
),水柱的最高点的坐标为(3, ),求此坐标系中抛物线对应的函数关系式(不要求写出自变量的取值范围).
),求此坐标系中抛物线对应的函数关系式(不要求写出自变量的取值范围). 水柱落地处刚好在最外轨道上,求当r为多少时,水池中安装的喷水龙头的个数最多?
水柱落地处刚好在最外轨道上,求当r为多少时,水池中安装的喷水龙头的个数最多?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com