
����Ŀ����һ���ı��ε�һ���Խ��߰��ı��ηֳ��������������Σ����ǰ������Խ��߽�����ı��εĺ�г�ߣ�����ı��ν�����г�ı��Σ������ξ��Ǻ�г�ı��Σ�

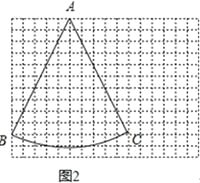
��1����ͼ1��������ABCD�У�AD��BC����BAD=120������C=75����BDƽ����ABC����֤��BD������ABCD�ĺ�г�ߣ�
��2����ͼ2����12��16������ͼ�ϣ�ÿ��С�����εı߳�Ϊ1����һ������BAC����A��B��C���ڸ���ϣ����ڴ������������������ͼ�ϸ���һ����D��ʹ����A��B��C��DΪ������ı��ε������Խ��߶��Ǻ�г�ߣ���������Ӧ�ĺ�г�ı��Σ�
��3���ı���ABCD�У�AB=AD=BC����BAD=90����AC���ı���ABCD�ĺ�г�ߣ�����BCD�Ķ�����
���𰸡���1��֤������������2������������3����BCD�Ķ���Ϊ135����90����45��.
��������
��1��Ҫ֤��BD���ı���ABCD�ĺ�г�ߣ�ֻ��Ҫ֤����ABD����BDC�ǵ��������μ���.
��2���������ε����ʻ��ϵĵ㵽����ľ�����ȣ�ֻҪD��![]() ������һ�㹹�ɵ��ı���ABDC���Ǻ�г�ı��Σ�����BC������BAC����һ����ACΪ���ĵ���������ACD�����ɵ��ı���ABCD���Ǻ�г�ı���.
������һ�㹹�ɵ��ı���ABDC���Ǻ�г�ı��Σ�����BC������BAC����һ����ACΪ���ĵ���������ACD�����ɵ��ı���ABCD���Ǻ�г�ı���.
��3����AC���ı���ABCD�ĺ�г�ߣ����Եó���ACD�ǵ��������Σ���ͼ4��ͼ5��ͼ6����������õȱ������ε����ʣ������ε����ʺ�30����ֱ�����������ʾͿ��������BCD�Ķ���.
��1����AD��BC�����ABC+��BAD=180������ADB=��DBC.
�ߡ�BAD=120�������ABC=60��.
��BDƽ����ABC�����ABD=��DBC=30��.
���ABD=��ADB.���ADB�ǵ���������.
����BCD�У���C=75������DBC=30�������BDC=��C=75��.���BCDΪ����������.
��BD������ABCD�ĺ�г��.
��2����������ͼΪ��ͼ2��ͼ3
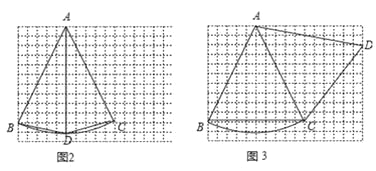
��3����AC���ı���ABCD�ĺ�г�ߣ����ACD�ǵ���������.
��AB=AD=BC���������������
��ͼ4����AD=ACʱ��
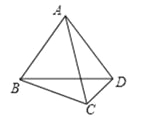
ͼ4
��AB=AC=BC����ACD=��ADC.
���ABC����������.���BAC=��BCA=60��.
�ߡ�BAD=90�������CAD=30��.
���ACD=��ADC=75��.���BCD=60��+75��=135��.
��ͼ5����AD=CDʱ��
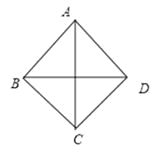
ͼ5
��AB=AD=BC=CD.
�ߡ�BAD=90�������ı���ABCD��������.
���BCD=90��.
��ͼ6����AC=CDʱ��
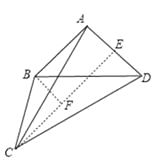
ͼ6
����C��CE��AD��E������B��BF��CE��F��
��AC=CD��CE��AD����AE=AD����ACE=��DCE.
�ߡ�BAD=��AEF=��BFE=90����
���ı���ABFE�Ǿ���.��BF=AE.
��AB=AD=BC����BF=BC.���BCF=30��.
��AB=BC�����ACB=��BAC.
��AB��CE�����BAC=��ACE.���ACB=��ACE=��BCF=15��.
���BCD=15���3=45��.
������������BCD�Ķ���Ϊ135����90����45��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
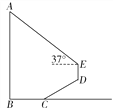
����Ŀ�������ģ���ͼ��ij��ѧ�С��Ϊ����ѧУ���AB�ĸ߶����������ǰ��2![]() m���ĵ�C��������б���¶�i��1��
m���ĵ�C��������б���¶�i��1��![]() ��б��CDǰ��4m�����D���ڵ�D�����ò�����������˶���A������Ϊ37�㣬���������ĸ�DEΪ1.5 m����֪A��B��C��D��E��ͬһƽ������AB��BC��AB��DE.�����AB�ĸ߶ȣ�(�ο����ݣ�sin37���
��б��CDǰ��4m�����D���ڵ�D�����ò�����������˶���A������Ϊ37�㣬���������ĸ�DEΪ1.5 m����֪A��B��C��D��E��ͬһƽ������AB��BC��AB��DE.�����AB�ĸ߶ȣ�(�ο����ݣ�sin37���![]() ��cos37���
��cos37���![]() ��tan37���
��tan37���![]() ����������������)
����������������)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
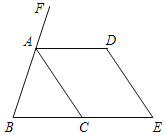
����Ŀ����ͼ�������н���У���д�ʵ������ɻ���ѧʽ��
��1����AD��BE������֪��
���B���ϣ� ��������
��2���ߡ�E+��������180�㣬����֪��
��AC��DE�� ������
��3����������������֪��
���ACB����DAC�� ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����ֱ��CD���O�����ڵ�C������AB���ӳ��߽��ڵ�E����C�ǻ�BF���е㣮
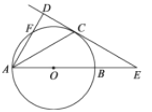
��1����֤��AD��CD��
��2������CAD=30������O�İ뾶Ϊ3��һֻ���ϴӵ�B����������BE--EC--��CB��������B��������������·��(�С�3.14��![]() ��1.73���������һλС����)
��1.73���������һλС����)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1,��ƽ��ֱ������ϵ��,ֱ��![]() ��������
��������![]() ����
����![]() ���㣬����
���㣬����![]() ,
,![]() .����������
.����������![]() �ύ�ڵ�
�ύ�ڵ�![]() ,��
,��![]() �ύ����һ��
�ύ����һ��![]() .
.

(1)��![]() ��ֵ���������ߵĽ���ʽ;
��ֵ���������ߵĽ���ʽ;
(2)��ͼ2.����![]() Ϊ�߶�
Ϊ�߶�![]() �ϵ�һ����(����
�ϵ�һ����(����![]() �غ�).�ֱ���
�غ�).�ֱ���![]() ��
��![]() Ϊб��,��ֱ��
Ϊб��,��ֱ��![]() ��ͬ��������ֱ����
��ͬ��������ֱ����![]() �͵���ֱ����
�͵���ֱ����![]() ,����
,����![]() ,��ȷ����
,��ȷ����![]() ������ʱ
������ʱ![]() �������.
�������.
(3)��ͼ3.����![]() ��
��![]() ,���߶�
,���߶�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ,ʹ����
,ʹ����![]() Ϊ���������������
Ϊ���������������![]() ����,������,��ֱ��д����
����,������,��ֱ��д����![]() ������;��������,��˵������.
������;��������,��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+c��a��0����ͼ��Ķ����ڵ�һ���ޣ��ҹ��㣨0��1���ͣ���1��0�������н��ۣ���ab��0����b2��4����0��a+b+c��2����0��b��1������x����1ʱ��y��0��������ȷ������___________.
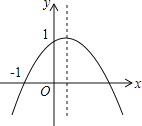
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ͼ�ζ��������Ϊ1�������ΰ�һ���Ĺ�����ɣ����У�ͼ1�����Ϊ1����������9����ͼ2�����Ϊ1����������14����![]() �����˹��ɣ�ͼ12�����Ϊ1�������εĸ���Ϊ
�����˹��ɣ�ͼ12�����Ϊ1�������εĸ���Ϊ![]() ����
����![]()

A.64B.60C.54D.50
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ��6����B��������A���Ҳ࣬��AB��14������M�ӵ�A��������ÿ��5����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt��t��0���룮
![]()
��1��д�������ϵ�B��ʾ������ ������M��ʾ������ �����ú�t��ʽ�ӱ�ʾ����
��2������N�ӵ�B��������ÿ��3����λ���ȵ��ٶ����������������˶�������M��Nͬʱ�������ʵ�M�˶�������ʱ�ϵ�N��
��3����PΪAM���е㣬FΪMB���е㣬��M���˶������У��߶�PF�ij����Ƿ����仯�����仯����˵�����ɣ������䣬������߶�PF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʵ��a��b�����ǿ�����min{a��b}��ʾa��b�����н�С����������min{3����1}����1��min{2��2}��2. ���Ƶأ�������y1��y2����x�ĺ�������y��min{y1�� y2}��ʾ����y1��y2����ȡС��������
��1����y1��x��y2��![]() ������y��min{x��
������y��min{x�� ![]() }��ͼ��Ӧ���� �е�ʵ�߲��֣�
}��ͼ��Ӧ���� �е�ʵ�߲��֣�

��2��������ͼ������ʵ���������y��min{(x��2)2�� (x��2)2}��ͼ��д����ͼ���������ͬ���ʣ�

�� ��
�� ��
�� ��
��3������y��min{(x��4)2�� (x��2)2}��ͼ����� �Գƣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com