
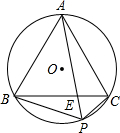
 如图,正△ABC内接于⊙O,P是劣弧BC上任意一点,PA与BC交于点E,有如下结论:
如图,正△ABC内接于⊙O,P是劣弧BC上任意一点,PA与BC交于点E,有如下结论:| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
分析 根据题意:易得△APC≌△BDC.即AP=BD,有PA=DB=PB+PD=PB+PC,①正确.同时可得:②错误;同理易得△PBE∽△PAC,故有PA•PE=PB•PC;④正确.由圆内接四边形的性质可得∠BPC=120゜,③正确;因为图中共有4对相似三角形,⑤错误.
解答 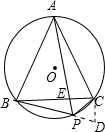 解:延长BP到D,使PD=PC,连接CD,可得∠CPD=∠BAC=60°,
解:延长BP到D,使PD=PC,连接CD,可得∠CPD=∠BAC=60°,
则△PCD为等边三角形,
∵△ABC为正三角形,
∴BC=AC
∵∠PBC=∠CAP,∠CPA=∠CDB,
∴△APC≌△BDC(AAS).
∴PA=DB=PB+PD=PB+PC,故①正确;
由(1)知△PBE∽△PAC,则$\frac{PA}{PC}$=$\frac{PB}{PE}$,$\frac{PA}{PB}$=$\frac{PC}{PE}$,$\frac{PA}{PB}$$+\frac{PA}{PC}$=$\frac{PC}{PE}$$+\frac{PB}{PE}$≠1,
∴②错误;
∵∠BAC=60°,
∴∠PBC=120°,故③正确;
∵∠CAP=∠EBP,∠BPE=∠CPA
∴△PBE∽△PAC,
∴$\frac{PA}{PB}$=$\frac{PC}{PE}$,
∴PA•PE=PB•PC,故④正确,
∵△ABE∽△CPE,△AEC∽△BEP,△ACE∽△APC,△APC∽△BPE,△ABE∽△APB,△CPE∽△APB共6对相似三角形,故⑤正确,
故选B.
点评 本题考查了全等三角形的判定与性质相似三角形的判定和性质,等腰三角形的性质,辅助线的作法是解题的关键.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:填空题
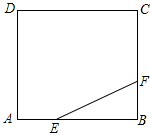 如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到BC边时,小球P所经过的路程为$\sqrt{5}$;当小球P第一次碰到AD边时,小球P所经过的路程为$\frac{5}{2}\sqrt{5}$;当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为$6\sqrt{5}n\;-5\sqrt{5}$.
如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到BC边时,小球P所经过的路程为$\sqrt{5}$;当小球P第一次碰到AD边时,小球P所经过的路程为$\frac{5}{2}\sqrt{5}$;当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为$6\sqrt{5}n\;-5\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
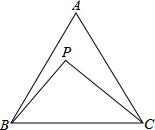 如图,等边三角形ABC中,点P在△ABC内部,且∠BPC=90°.若AB=7,CP=2$\sqrt{7}$,则tan∠ACP=$\frac{24-7\sqrt{3}}{49}$.
如图,等边三角形ABC中,点P在△ABC内部,且∠BPC=90°.若AB=7,CP=2$\sqrt{7}$,则tan∠ACP=$\frac{24-7\sqrt{3}}{49}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
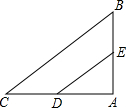 如图,△ABC中,AB=3,AC=4,BC=5,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( )
如图,△ABC中,AB=3,AC=4,BC=5,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( )| A. | 相切 | B. | 相交 | C. | 相离 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
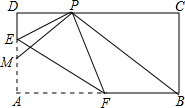 如图,已知在矩形ABCD中,AB=4,BC=2,点M,E在AD上,点F在边AB上,并且DM=1,现将△AEF沿着直线EF折叠,使点A落在边CD上的点P处,则当PB+PM的和最小时,ME的长度为( )
如图,已知在矩形ABCD中,AB=4,BC=2,点M,E在AD上,点F在边AB上,并且DM=1,现将△AEF沿着直线EF折叠,使点A落在边CD上的点P处,则当PB+PM的和最小时,ME的长度为( )| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 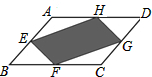 | B. | 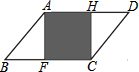 | ||
| C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com