
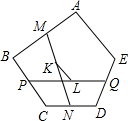
 如图,任意五边形ABCDE,M、N、P、Q分别为AB、CD、BC、DE的中点,K、L分别为MN、PQ的中点,
如图,任意五边形ABCDE,M、N、P、Q分别为AB、CD、BC、DE的中点,K、L分别为MN、PQ的中点,| 1 | 4 |
 证明:连接BE,取其中点R,连接MR,RN,PR,PN,NQ,RQ.
证明:连接BE,取其中点R,连接MR,RN,PR,PN,NQ,RQ.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |


科目:初中数学 来源: 题型:阅读理解
 (2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?
(2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 180° |
| n |
| 180° |
| n |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 1 |
| 4 |

查看答案和解析>>
科目:初中数学 来源:2001年全国初中数学竞赛(天津赛区)初赛试卷(解析版) 题型:解答题
 AE.
AE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com