
【题目】如图,在△ABC中,∠ACB=3∠B,AB=10,AC=4,AD平分∠BAC,交BC于点D,CE⊥AD于E,则CE= ______.

 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】小王剪了两张直角三角形纸片,进行了如下的操作:
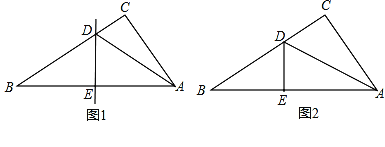
操作一:如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6cm,BC=8cm,可求得△ACD的周长为 ;
(2)如果∠CAD:∠BAD=4:7,可求得∠B的度数为 ;
操作二:如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=9cm,BC=12cm,请求出CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
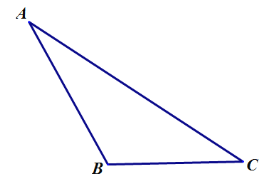
【题目】按照下列要求画图并填空:
(1)画出边![]() 的高,垂足为
的高,垂足为![]() ,则点
,则点![]() 到直线
到直线![]() 的距离是线段______的长.
的距离是线段______的长.
(2)用直尺和圆规作出![]() 的边
的边![]() 的垂直平分线
的垂直平分线![]() ,分别交直线
,分别交直线![]() 、
、![]() 于点
于点![]() 、
、![]() ,联结
,联结![]() ,则线段
,则线段![]() 是
是![]() 的______(保留作图痕迹).
的______(保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结合“爱市西,爱生活,会创新”的主题,某同学设计了一款“地面霓虹探测灯”,增加美观的同时也为行人的夜间行路带去了方便.他的构想如下:在平面内,如图1所示,灯![]() 射线从
射线从![]() 开始顺时针旋转至
开始顺时针旋转至![]() 便立即回转,灯
便立即回转,灯![]() 射线从
射线从![]() 开始顺时针旋转至
开始顺时针旋转至![]() 便立即回转,两灯不停交叉照射巡视.若灯
便立即回转,两灯不停交叉照射巡视.若灯![]() 转动的速度是每秒2度,灯
转动的速度是每秒2度,灯![]() 转动的速度是每秒1度.假定主道路是平行的,即
转动的速度是每秒1度.假定主道路是平行的,即![]() ,且
,且![]() .
.
(1)填空:![]() ______
______![]() ;
;
(2)若灯![]() 射线先转动60秒,灯
射线先转动60秒,灯![]() 射线才开始转动,在灯
射线才开始转动,在灯![]() 射线到达
射线到达![]() 之前,
之前,![]() 灯转动几秒,两灯的光束互相平行?
灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯![]() 射线到达
射线到达![]() 之前,若射出的光束交于点
之前,若射出的光束交于点![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,则在转动过程中,请探究
,则在转动过程中,请探究![]() 与
与![]() 的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
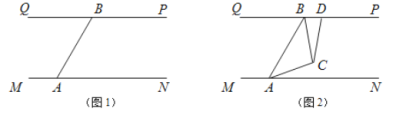
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14.
![]()
(1)写出数轴上点B表示的数;
(2)若点M、N分别是线段AO、BO的中点,求线段MN的长;
(3)若动点P从点A出发.以每秒5个单位长度的速度沿数轴向左匀速运动,动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.问点P运动多少秒时追上点Q?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好治理西太湖水质,保护环境,市治污公司决定购买10 台污水处理设备,现有A、B两种型号的设备,其中每台的价格,月处理污水量如下表:

经调查:购买-台A型设备比购买一-台B型设备多2万元,购买2台A型设备比购买4台B型设备少4万元.
(1)求a、b的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过47万元,并且该月要求处理西太湖的污水量不低于1860 吨,则有哪几种购买方案?请指出最省钱的一种购买方案,并指出相应的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数 ![]() 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点. 
(1)求一次函数的解析式;
(2)根据图象直接写出 ![]() 的x的取值范围;
的x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于点A,B,与y轴交于点C,其中点A在y轴的左侧,点C在x轴的下方,且OA=OC=5.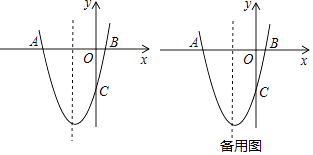
(1)求抛物线对应的函数解析式;
(2)点P为抛物线对称轴上的一动点,当PB+PC的值最小时,求点P的坐标;
(3)在(2)条件下,点E为抛物线的对称轴上的动点,点F为抛物线上的动点,以点P、E、F为顶点作四边形PEFM,当四边形PEFM为正方形时,请直接写出坐标为整数的点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com