
 天水历史悠久,文物古迹星罗棋布,是中国历史文化名城,也是中国优秀旅游城市.如图是秦州区的部分旅游景点,请你以中心广场为坐标原点建立坐标系,并写出各景点的坐标:
天水历史悠久,文物古迹星罗棋布,是中国历史文化名城,也是中国优秀旅游城市.如图是秦州区的部分旅游景点,请你以中心广场为坐标原点建立坐标系,并写出各景点的坐标:科目:初中数学 来源: 题型:选择题
 如图,直线y=-$\frac{\sqrt{3}}{3}$x+b与y轴交于点A,与双曲线y=$\frac{k}{x}$在第一象限交于B、C两点,且AB•AC=4,则k=( )
如图,直线y=-$\frac{\sqrt{3}}{3}$x+b与y轴交于点A,与双曲线y=$\frac{k}{x}$在第一象限交于B、C两点,且AB•AC=4,则k=( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
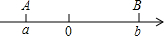 阅读下面材料:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.回答下列问题:
阅读下面材料:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com