
分析 (1)利用目前,他所养的这两种兔子数量相同,得出等式求出即可;
(2)利用一年前买入的A种兔子数量多于B种兔子数量,得出不等式求出即可;
(3)利用总共获利不低于280元,卖A种兔子可获利15元/只,卖B种兔子可获利6元/只,得出不等关系,进而利用A种兔子的数量取值范围得出即可.
解答 解:(1)∵一年前买入了A、B两种兔子共46只,目前,他所养的这两种兔子数量相同,且A种兔子的数量比买入时减少了3只,B种兔子的数量比买入时减少a只,
∴设一年前A种兔子x只,则B种兔子(46-x)只,
∴x-3=46-x-a,
解得:x=$\frac{49-a}{2}$,
目前A、B两种兔子共有:46-3-a=43-a,
故答案为:$\frac{49-a}{2}$,43-a;
(2)由题意得出:$\frac{49-a}{2}$>$\frac{43+a}{2}$,
解得:a<3,
由题意得:a,$\frac{49-a}{2}$,$\frac{43+a}{2}$应为正整数,
当a=1时,符合题意,即目前A、B两种兔子有42只;
当a=2时,$\frac{49-a}{2}$,$\frac{43+a}{2}$为分数,不合题意;
∴当a=1时,A、B两种兔子有42只;
(3)设李大爷卖出A种兔子y只,则卖出B种兔子(30-y)只,由题意得出:
15y+(30-y)×6≥280,
解得:y≥$\frac{100}{9}$,
又∵卖出的A种兔子少于15只,即$\frac{100}{9}$≤y<15,
∵y是整数,
∴y=12,13,14,即李大爷有三种卖兔方案:
方案一:卖出的A种兔子12只,B种兔子18只,可获利12×15+18×6=288(元),
方案二:卖出的A种兔子13只,B种兔子17只,可获利13×15+17×6=297(元),
方案三:卖出的A种兔子14只,B种兔子16只,可获利14×15+16×6=306(元),
显然,方案三获利最大,最大利润为306元.
点评 此题主要考查了一元一次不等式的应用,根据题意得出正确的不等关系是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | M<P | B. | M>P | C. | M≥P | D. | 不确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
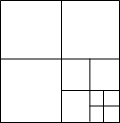 连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…重复这样的操作,则5次操作后右下角的小正方形面积是( )
连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…重复这样的操作,则5次操作后右下角的小正方形面积是( )| A. | ($\frac{1}{2}$)5 | B. | 1-($\frac{1}{4}$)5 | C. | $\frac{1}{5}$ | D. | ($\frac{1}{4}$)5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.708×10-6米 | B. | 7.08×10-7米 | C. | 70.8×10-8米 | D. | 708×10-9米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
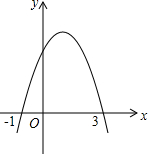 二次函数y=ax2+bx+c的图象如图所示,则下列判断中错误的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列判断中错误的是( )| A. | 图象的对称轴是直线x=1 | |
| B. | 当-1<x<3时,y<0 | |
| C. | 一元二次方程ax2+bx+c=0的两个根是-1,3 | |
| D. | 当x>1时,y随x的增大而减小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com