
分析 (1)首先根据题意求出x的取值范围,结合x为整数,即可判断出商家的几种进货方案;
(2)令总利润为W,根据利润=售价-成本列出W与x的函数关系式W=30(x-9)2+9570,求出二次函数的最值即可.
解答 解:(1)设购买羽绒服x件,则购买皮衣(20-x)件,则:
$\left\{\begin{array}{l}{x≥20-x}\\{-20x+150≥1240}\\{0<x≤20且x为整数}\end{array}\right.$,
∴10≤x≤13且为整数,
∴该店主有4种进货方案:
羽绒服10件,皮衣10件;
羽绒服11件,皮衣9件;
羽绒服12件,皮衣8件;
羽绒服13件,皮衣7件;
(2)设购买羽绒服x件,利润为W元,则
W=(1760+20x-1500)x+(1700+10(20-x)-1300)(20-x)
=30(x-9)2+9570(10≤x≤13且为整数)
∵a=30>0,
∴当10≤x≤13且为整数是,W随x的增大而增大,
∴当x=13时,最大利润为10050元.
答:当采购羽绒服13件时,有最大利润为10050元.
点评 本题主要考查二次函数的应用的知识点,解答本题的关键是明确销售单价与销售件数之间的函数关系式,会表达单件的利润及总利润,此题难度一般.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| -0.87 | +1 | -1.2 | 0 | -0.7 | +0.6 | -0.4 | -0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
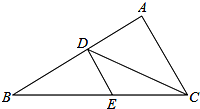 如图所示,在△ABC中,CD平分∠ACB,DE∥AC.
如图所示,在△ABC中,CD平分∠ACB,DE∥AC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
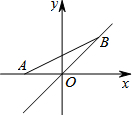 如图,点A的坐标为(-1,0),点B在直线y=x上运动,已知直线y=x与x轴的夹角为45°,则当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-1,0),点B在直线y=x上运动,已知直线y=x与x轴的夹角为45°,则当线段AB最短时,点B的坐标为( )| A. | (0,0) | B. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) | C. | (-$\frac{1}{2}$,-$\frac{1}{2}$) | D. | (-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com