
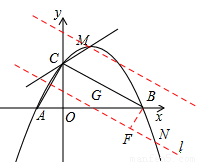
如图14,已知点A(-1,0),B(4,0),点C在y轴的正半轴上,且∠ACB=900,抛物线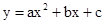 经过A、B、C三点,其顶点为M.
经过A、B、C三点,其顶点为M.
求抛物线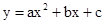 的解析式;
的解析式;
试判断直线CM与以AB为直径的圆的位置关系,并加以证明;
在抛物线上是否存在点N,使得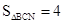 ?如果存在,那么这样的点有几个?如果不存在,请说明理由。
?如果存在,那么这样的点有几个?如果不存在,请说明理由。
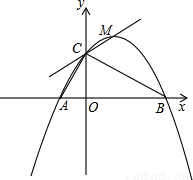
解:(1)Rt△ACB中,OC⊥AB,AO=1,BO=4,
∴△ACO∽△ABO 。∴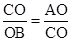 ,∴OC2=OA•OB=4。
,∴OC2=OA•OB=4。
∴OC=2。∴点C(0,2)。
∵抛物线 经过A、B两点,
经过A、B两点,
∴设抛物线的解析式为: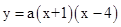 ,将C点代入上式,得:
,将C点代入上式,得:
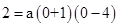 ,解得
,解得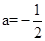 。
。
∴抛物线的解析式: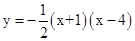 ,即
,即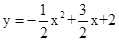 。
。
(2)直线CM与以AB为直径的圆相切。理由如下:
如图,设抛物线的对称轴与x轴的交点为D,连接CD。

由于A、B关于抛物线的对称轴对称,则点D为Rt△ABC斜边AB的中点,CD=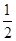 AB。
AB。
由(1)知: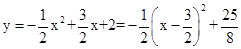 ,
,
则点M(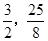 ),ME=
),ME=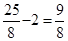 。
。
而CE=OD=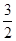 ,OC=2,∴ME:CE=OD:OC。
,OC=2,∴ME:CE=OD:OC。
又∵∠MEC=∠COD=90°,∴△COD∽△CEM。∴∠CME=∠CDO。
∴∠CME+∠CDM=∠CDO+∠CDM=90°。∠DCM=90°。
∵CD是⊙D的半径,∴直线CM与以AB为直径的圆相切。
(3)由B(4,0)、C(0,2)得:BC= ,
,
则: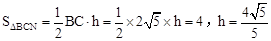 。
。
过点B作BF⊥BC,且使BF=h=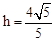 ,过F作直线l∥BC交x轴于G。
,过F作直线l∥BC交x轴于G。
Rt△BFG中,sin∠BGF=sin∠CBO= ,
,
BG=BF÷sin∠BGF=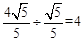 。
。
∴G(0,0)或(8,0)。
易知直线BC:y=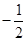 x+2,则可设直线l:y=
x+2,则可设直线l:y=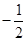 x+b,
x+b,
将G点坐标代入,得:b=0或b=4,则:
直线l:y=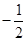 x或y=
x或y=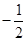 x+4;
x+4;
联立抛物线的解析式,得:
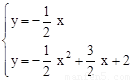 ,或
,或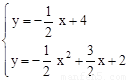 。
。
解得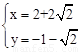 或
或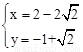 或
或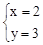 。
。
∴抛物线上存在点N,使得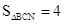 ,这样的点有3个:
,这样的点有3个:
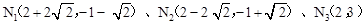 。
。
【解析】二次函数综合题,待定系数法,曲线上点的坐标与方程的关系,相似三角形的判定和性质,二次函数的性质,直线与的位置关系,平行线的性质。
【分析】(1)Rt△ACB中,OC⊥AB,利用相似三角形能求出OC的长,即可确定C点坐标,再利用待定系数法能求出该抛物线的解析式。
(2)证明CM垂直于过点C的半径即可。
(3)先求出线段BC的长,根据△BCN的面积,可求出BC边上的高,那么做直线l,且直线l与直线BC的长度正好等于BC边上的高,那么直线l与抛物线的交点即为符合条件的N点。


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
 全,是否将此人行道封上?(在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域)
全,是否将此人行道封上?(在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域)查看答案和解析>>
科目:初中数学 来源: 题型:
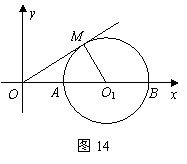
如图14,已知半径为1的![]() 与
与![]() 轴交于
轴交于![]() 两点,
两点,![]() 为
为![]() 的切线,切点为
的切线,切点为![]() ,圆心
,圆心![]() 的坐标为
的坐标为![]() ,二次函数
,二次函数![]() 的图象经过
的图象经过![]() 两点.
两点.
(1)求二次函数的解析式;
(2)求切线![]() 的函数解析式;
的函数解析式;
(3)线段![]() 上是否存在一点
上是否存在一点![]() ,使得以
,使得以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.若存在,请求出所有符合条件的点
相似.若存在,请求出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(四川内江卷)数学(带解析) 题型:解答题
如图14,已知点A(-1,0),B(4,0),点C在y轴的正半轴上,且∠ACB=900,抛物线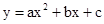 经过A、B、C三点,其顶点为M.
经过A、B、C三点,其顶点为M.
求抛物线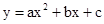 的解析式;
的解析式;
试判断直线CM与以AB为直径的圆的位置关系,并加以证明;
在抛物线上是否存在点N,使得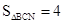 ?如果存在,那么这样的点有几个?如果不存在,请说明理由。
?如果存在,那么这样的点有几个?如果不存在,请说明理由。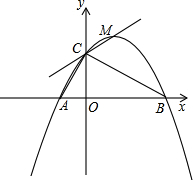
查看答案和解析>>
科目:初中数学 来源: 题型:
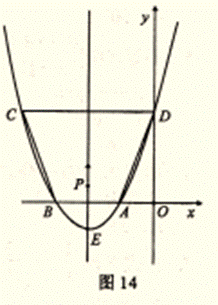
如图14,已知抛物线![]() 与x轴的一个交点A的坐标为(-1,0),对称轴为直线 x = 2.
与x轴的一个交点A的坐标为(-1,0),对称轴为直线 x = 2.
(1)求抛物线与x轴的另一个交点B的坐标;
(2)点D是抛物线与y轴的交点,点C是抛物线上的另一点。已知以AB为一底边的梯形ABCD的面积为9.求此抛物线的解析式,并指出顶点E的坐标;
(3)点P是(2)中抛物线对称轴上一动点,且以1个单位/秒的速度从此抛物线的顶点E向上运动。设点P运动的时间为t秒。
①当t为 秒是,△PAD的周长最小?当t为 秒时,△PAD是以AD为腰的等腰三角形?(结果保留根号)
②点P在运动过程中,是否存在一点P,使△PAD是以AD为斜边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com