
【题目】计算题:计算
(1)计算:( ![]() )﹣1﹣3tan30°+(1﹣π)0
)﹣1﹣3tan30°+(1﹣π)0 ![]() .
.
(2)解分式方程: ![]() =
= ![]() ﹣1.
﹣1.
【答案】
(1)解:原式=2﹣3× ![]() +1+2
+1+2 ![]()
=3+ ![]()
(2)解:方程的两边同乘(x+1)(x﹣1),得2(x﹣1)=x(x+1)﹣(x+1(x﹣1),
∴2x﹣2=x2+x﹣x2+1,
解得x=3.
检验:把x=3代入(x+1)(x﹣1)=8≠0,即x=3是原分式方程的解,
∴原方程的解:x=3
【解析】负整数幂是其正整数幂的倒数;非零数幂的0次幂等于1;分式方程的基本解法是去分母法,要检验.
【考点精析】通过灵活运用零指数幂法则和整数指数幂的运算性质,掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数)即可以解答此题.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】某商人制成了一个如图所示的转盘,取名为“开心大转盘”,游戏规定:参与者自由转动转盘,转盘停止后,若指针指向字母“A”,则收费2元,若指针指向字母“B”,则奖励3元;若指针指向字母“C”,则奖励1元.一天,前来寻开心的人转动转盘80次,你认为该商人是盈利的可能性大还是亏损的可能性大?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
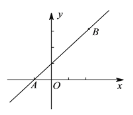
【题目】如图,已知直线y1经过点A(-1,0)与点B(2.3),另一条直线y2经过点B,且与x轴交于点P(m.0).
(1)求直线y1的解析式;
(2)若三角形ABP的面积为![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长一定的正方形ABCD,Q为CD上一个动点,AQ交BD于点M,过M作MN⊥AQ交BC于点N,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;②MP= ![]() BD;③BN+DQ=NQ;④
BD;③BN+DQ=NQ;④ ![]() 为定值.其中一定成立的是 .
为定值.其中一定成立的是 .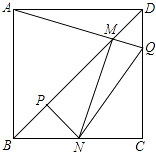
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了扩大内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定对购买彩电的农户实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图①所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益z(元)会相应降低且z与x之间也大致满足如图②所示的一次函数关系.
(1)在政府未出台补贴措施前,该商场销售彩电的总收益额为多少元?
(2)在政府补贴政策实施后,分别求出该商场销售彩电台数y和每台家电的收益z与政府补贴款额x之间的函数关系式;
(3)要使该商场销售彩电的总收益w(元)最大,政府应将每台补贴款额x定为多少并求出总收益w的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,把一张正方形纸片对折得到长方形ABCD,再沿∠ADC的平分线DE折叠,如图2,点C落在点C′处,最后按图3所示方式折叠,使点A落在DE的中点A′处,折痕是FG,若原正方形纸片的边长为9cm,则FG=_____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com