
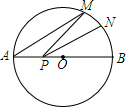
 如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=40°,N是弧MB的中点,P是直径AB上的一动点,PM+PN的最小值为( )
如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=40°,N是弧MB的中点,P是直径AB上的一动点,PM+PN的最小值为( )| A. | 4$\sqrt{3}$+1 | B. | 4$\sqrt{3}$ | C. | 4$\sqrt{2}$+1 | D. | 5 |
分析 作点N关于AB的对称点C,连接MC交AB于点P,则P点就是所求作的点,求出∠COM=120°,进而求出CM的长,CM的长度即PM+PN的最小值.
解答 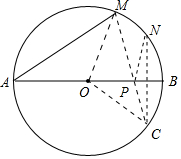 解:作点N关于AB的对称点C,连接MC交AB于点P,则P点就是所求作的点.
解:作点N关于AB的对称点C,连接MC交AB于点P,则P点就是所求作的点.
此时PM+PN最小,且等于MC的长.
连接OM,OC,
∵∠MAB=40°,
∴∠MOB=80°,
∴$\widehat{BM}$的度数是80°,
则$\widehat{NB}$的度数是40°,
根据垂径定理得$\widehat{CB}$的度数是40°,
则∠NOC=120°,
∵AB=8
∴OM=OC=4,
∴∠OAM=∠OMC=30°,
∴MC=4$\sqrt{3}$.
∴PM+PN的最小值为4$\sqrt{3}$,
故选B.
点评 此题主要考查了轴对称-最短路线问题,垂径定理,直角三角形的性质等,确定点P的位置是本题的关键.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:填空题
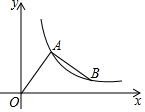 如图,在平面直角坐标系中,点A(2,m)是第一象限内一点,连接OA,将OA绕点A逆时针旋转90°得到线段AB,若反比例函数y=$\frac{k}{x}$(x>0)的图象恰好同时经过点A、B,则k的值为2+2$\sqrt{5}$.
如图,在平面直角坐标系中,点A(2,m)是第一象限内一点,连接OA,将OA绕点A逆时针旋转90°得到线段AB,若反比例函数y=$\frac{k}{x}$(x>0)的图象恰好同时经过点A、B,则k的值为2+2$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
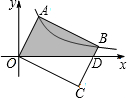 如图,在直角坐标系中,矩形OABC的顶点A、B在双曲线y=$\frac{k}{x}$( x>0)上,BC与x轴交于点D.若点A的坐标为(2,4),则点D的坐标为( )
如图,在直角坐标系中,矩形OABC的顶点A、B在双曲线y=$\frac{k}{x}$( x>0)上,BC与x轴交于点D.若点A的坐标为(2,4),则点D的坐标为( )| A. | ($\frac{22}{3}$,0) | B. | ($\frac{15}{2}$,0) | C. | ($\frac{68}{9}$,0) | D. | ($\frac{48}{5}$,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3a+a=-2a | B. | a6÷a3=a2 | C. | $\sqrt{8}$+$\sqrt{2}$=10 | D. | (-2a2b3)2=4a4b5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 数据1,2,3,2,5的中位数是3 | |
| B. | 对我市某社区每天丢弃塑料袋数量的调查,应采用普查的方式 | |
| C. | 在同一年出生的367名学生中,至少有两人的生日是同一天 | |
| D. | 若甲组数据的方差是0.15,乙组数据的方差是0.21,则乙组数据比甲组数据稳定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com