解:如右图所示,
(1)∵AB是直径,
∴∠C=90°,
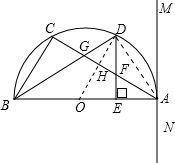
∴∠CBA+∠BAC=90°,
又∵∠MAC=∠ABC,
∴∠MAC+∠CAB=90°,
即∠BAM=90°,
∴OA⊥MN,
∴MN是⊙O的切线;
(2)连接OD交AC于H,
∵D是AC中点,
∴OD⊥AC,AH=

AC,
∵∠DOE=∠AOH,∠OHA=∠OED=90°,OA=OD,
∴△OAH≌△ODE,
∴DE=AH=

AC;
(3)连接AD,
由(2)知△OAH≌△ODE,
∴∠ODE=∠OAH,
又∵OA=OD,
∴∠ODA=∠OAD,
∴∠ODA-∠ODE=∠OAD-∠OAH,
即∠FDA=∠FAD,
∴FD=FA,
∵AB是直径,
∴∠BDA=90°,
∴∠FDA+∠GDF=90°,∠DAF+∠DGF=90°,
∴∠GDF=∠DGF,
∴FG=DF,
∴FG=FA=FD,
∴S
△DGF=

S
△ADG,
易证△BCG∽△ADG,
∴S
△BCG:S
△ADG=(
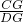
)
2=(

)
2,
∴S
△BCG=
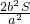
.
分析:(1)由于AB是直径,那么∠C=90°,于是∠CBA+∠BAC=90°,而∠MAC=∠ABC,可证∠MAC+∠CAB=90°,即∠BAM=90°,可证MN是⊙O的切线;
(2)连接OD交AC于H,由于D是AC中点,那么OD⊥AC,AH=

AC,而∠DOE=∠AOH,∠OHA=∠OED=90°,OA=OD,易证△OAH≌△ODE,从而有DE=AH=

AC;
(3)连接AD,由(2)中△OAH≌△ODE,可知∠ODE=∠OAH,再结合OA=OD,易证∠FDA=∠FAD,可得FD=FA,而AB是直径,那么∠ADB=90°,易证FG=DF,从而有FG=FA=FD,那么S
△DGF=

S
△ADG,而根据图易知△BCG∽△ADG,于是有S
△BCG:S
△ADG=(
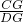
)
2=(

)
2,易求S
△BCG.
点评:本题考查了切线的判定和性质、全等三角形的判定和性质、垂径定理、相似三角形的判定和性质.解题的关键是作辅助线,如连接OD交AC于H,连接AD,构造直角三角形和等腰三角形.

 如图,△ABC内接于半圆,圆心为O,AB是直径,过A作直线MN,若∠MAC=∠ABC.
如图,△ABC内接于半圆,圆心为O,AB是直径,过A作直线MN,若∠MAC=∠ABC. AC;
AC;
 AC,
AC, AC;
AC; S△ADG,
S△ADG,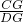 )2=(
)2=( )2,
)2,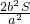 .
. AC,而∠DOE=∠AOH,∠OHA=∠OED=90°,OA=OD,易证△OAH≌△ODE,从而有DE=AH=
AC,而∠DOE=∠AOH,∠OHA=∠OED=90°,OA=OD,易证△OAH≌△ODE,从而有DE=AH= AC;
AC; S△ADG,而根据图易知△BCG∽△ADG,于是有S△BCG:S△ADG=(
S△ADG,而根据图易知△BCG∽△ADG,于是有S△BCG:S△ADG=(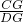 )2=(
)2=( )2,易求S△BCG.
)2,易求S△BCG.

 53随堂测系列答案
53随堂测系列答案 21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.
21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.