
°æƒø°ø‘⁄“ª∏ˆ≤ªÕ∏√˜µƒø⁄¥¸¿Ô◊∞”–÷ª”–—’…´≤ªÕ¨µƒ∫⁄°¢∞◊¡Ω÷÷—’…´µƒ«Úπ≤10÷ª£¨ƒ≥—ßœ∞–°◊È◊ˆ√˛«Ú µ—È£¨Ω´«ÚΩ¡‘»∫Û¥”÷–Àʪ˙√˛≥ˆ“ª∏ˆ«Úº«œ¬—’…´£¨‘Ÿ∞—À¸∑≈ªÿ¥¸÷–£¨≤ª∂œ÷ÿ∏¥£Æœ¬±Ì «ªÓ∂ØΩ¯––÷–µƒ“ª◊ÈÕ≥º∆ ˝æð£∫
√˛«Úµƒ¥Œ ˝ | 100 | 150 | 200 | 500 | 800 | 1000 |
√˛µΩ∞◊«Úµƒ¥Œ ˝ | 58 | 96 | 116 | 295 | 484 | 601 |
√˛µΩ∞◊«Úµƒ∆µ¬ | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
£®1£©«Îπ¿º∆£∫µ±![]() ∫Ð¥Û ±£¨√˛µΩ∞◊«Úµƒ∆µ¬ Ω´ª·Ω”Ω¸°° °°£ª£®±£¡Ù∂˛∏ˆ”––ß ˝◊÷£©
∫Ð¥Û ±£¨√˛µΩ∞◊«Úµƒ∆µ¬ Ω´ª·Ω”Ω¸°° °°£ª£®±£¡Ù∂˛∏ˆ”––ß ˝◊÷£©
£®2£© ‘π¿À„ø⁄¥¸÷–∫⁄°¢∞◊¡Ω÷÷—’…´µƒ«Ú∏˜”–∂ý…Ÿ÷ª£ø
£®3£©«Îª≠ ˜◊¥ÕºªÚ¡–±Ìº∆À„£∫¥”÷–“ª¥Œ√˛¡Ω÷ª«Ú£¨’‚¡Ω÷ª«Ú—’…´≤ªÕ¨µƒ∏≈¬ «∂ý…Ÿ£ø
°æ¥∞∏°ø£®1£©0.60£ª£®2£©∫⁄«Ú”–4÷ª£¨∞◊«Ú”–6÷ª£ª£®3£©¥∞∏º˚Ω‚Œˆ.
°æΩ‚Œˆ°ø
£®1£©π€≤ϱÌ∏Ò£¨º¥ø…µ√µ±n∫Ð¥Û ±£¨√˛µΩ∞◊«Úµƒ∆µ¬ Ω´ª·Ω”Ω¸0.60£ª
£®2£©∏˘æð£®1£©ø…µ√∞◊«Ú’º60%£¨º¥ø…«Ûµ√ø⁄¥¸÷–∫⁄°¢∞◊¡Ω÷÷—’…´µƒ«Ú∏˜”–∂ý…Ÿ÷ª£ª
£®3£©¡–±Ì«Ûµ√À˘”–µ»ø…ƒÐµƒΩ·π˚”Î¥”÷–“ª¥Œ√˛¡Ω÷ª«Ú£¨’‚¡Ω÷ª«Ú—’…´≤ªÕ¨µƒ«Èøˆ£¨º¥ø…∏˘æð∏≈¬ π´ Ω«ÛΩ‚£Æ
Ω‚£∫£®1£©”…±Ì∏Ò÷– ˝æðø…÷™£¨µ±![]() ∫Ð¥Û ±£¨√˛µΩ∞◊«Úµƒ∆µ¬ Ω´ª·Ω”Ω¸0.60£ª
∫Ð¥Û ±£¨√˛µΩ∞◊«Úµƒ∆µ¬ Ω´ª·Ω”Ω¸0.60£ª
£®2£©°þ10°¡0.60=6£¨10-6=4£¨
°ý∫⁄«Ú”–4÷ª£¨∞◊«Ú”–6÷ª£ª
£®3£©¡–±Ìµ√£∫
∫⁄ | ∫⁄ | ∫⁄ | ∫⁄ | ∞◊ | ∞◊ | ∞◊ | ∞◊ | ∞◊ | ∞◊ | |
∫⁄ | ∫⁄∫⁄ | ∫⁄∫⁄ | ∫⁄∫⁄ | ∞◊∫⁄ | ∞◊∫⁄ | ∞◊∫⁄ | ∞◊∫⁄ | ∞◊∫⁄ | ∞◊∫⁄ | |
∫⁄ | ∫⁄∫⁄ | ∫⁄∫⁄ | ∫⁄∫⁄ | ∞◊∫⁄ | ∞◊∫⁄ | ∞◊∫⁄ | ∞◊∫⁄ | ∞◊∫⁄ | ∞◊∫⁄ | |
∫⁄ | ∫⁄∫⁄ | ∫⁄∫⁄ | ∫⁄∫⁄ | ∞◊∫⁄ | ∞◊∫⁄ | ∞◊∫⁄ | ∞◊∫⁄ | ∞◊∫⁄ | ∞◊∫⁄ | |
∫⁄ | ∫⁄∫⁄ | ∫⁄∫⁄ | ∫⁄∫⁄ | ∞◊∫⁄ | ∞◊∫⁄ | ∞◊∫⁄ | ∞◊∫⁄ | ∞◊∫⁄ | ∞◊∫⁄ | |
∞◊ | ∫⁄∞◊ | ∫⁄∞◊ | ∫⁄∞◊ | ∫⁄∞◊ | ∞◊∞◊ | ∞◊∞◊ | ∞◊∞◊ | ∞◊∞◊ | ∞◊∞◊ | |
∞◊ | ∫⁄∞◊ | ∫⁄∞◊ | ∫⁄∞◊ | ∫⁄∞◊ | ∞◊∞◊ | ∞◊∞◊ | ∞◊∞◊ | ∞◊∞◊ | ∞◊∞◊ | |
∞◊ | ∫⁄∞◊ | ∫⁄∞◊ | ∫⁄∞◊ | ∫⁄∞◊ | ∞◊∞◊ | ∞◊∞◊ | ∞◊∞◊ | ∞◊∞◊ | ∞◊∞◊ | |
∞◊ | ∫⁄∞◊ | ∫⁄∞◊ | ∫⁄∞◊ | ∫⁄∞◊ | ∞◊∞◊ | ∞◊∞◊ | ∞◊∞◊ | ∞◊∞◊ | ∞◊∞◊ | |
∞◊ | ∫⁄∞◊ | ∫⁄∞◊ | ∫⁄∞◊ | ∫⁄∞◊ | ∞◊∞◊ | ∞◊∞◊ | ∞◊∞◊ | ∞◊∞◊ | ∞◊∞◊ | |
∞◊ | ∫⁄∞◊ | ∫⁄∞◊ | ∫⁄∞◊ | ∫⁄∞◊ | ∞◊∞◊ | ∞◊∞◊ | ∞◊∞◊ | ∞◊∞◊ | ∞◊∞◊ |
![]() “ªπ≤”–90÷÷µ»ø…ƒÐµƒΩ·π˚£¨¥”÷–“ª¥Œ√˛¡Ω÷ª«Ú£¨’‚¡Ω÷ª«Ú—’…´≤ªÕ¨µƒ”–48÷÷«Èøˆ£¨
“ªπ≤”–90÷÷µ»ø…ƒÐµƒΩ·π˚£¨¥”÷–“ª¥Œ√˛¡Ω÷ª«Ú£¨’‚¡Ω÷ª«Ú—’…´≤ªÕ¨µƒ”–48÷÷«Èøˆ£¨
![]() £®¡Ω÷ª«Ú—’…´≤ªÕ¨£©
£®¡Ω÷ª«Ú—’…´≤ªÕ¨£©![]() £Æ
£Æ


 —ß∂¯”≈œŒΩ”ΩÃ≤ƒƒœæ©¥Û—ß≥ˆ∞Ê…Áœµ¡–¥∞∏
—ß∂¯”≈œŒΩ”ΩÃ≤ƒƒœæ©¥Û—ß≥ˆ∞Ê…Áœµ¡–¥∞∏ –°—ßøŒÃ√◊˜“µœµ¡–¥∞∏
–°—ßøŒÃ√◊˜“µœµ¡–¥∞∏ Ω≤© ø“ªµ„»´Õ®œµ¡–¥∞∏
Ω≤© ø“ªµ„»´Õ®œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øΩ‚œ¬¡–∑Ω≥Ã
(1)£®x©Å8£©£®x©Å1£©=©Å12£ª
(2)3£®x©Å5£©2=2£®5©Åx£©£Æ
(3)y2£≠7y£´6£Ω0£ª
(4)2x2£≠4x£≠3£Ω0£ª
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™‘ˆ«ø—ß…˙µƒ…ÌÃÂÀÿ÷ £¨Ã©–À –ΩÔ˝––’˛≤ø√≈πÊ∂®—ß…˙√øÃÏ≤Œº”ªßÕ‚ªÓ∂صƒ∆Ωæ˘ ±º‰≤ª…Ÿ”⁄1–° ±£ÆŒ™¡ÀΩ‚—ß…˙≤Œº”ªßÕ‚ªÓ∂صƒ«Èøˆ£¨∂‘≤ø∑÷—ß…˙≤Œº”ªßÕ‚ªÓ∂صƒ ±º‰Ω¯––≥È—˘µ˜≤È£¨≤¢Ω´µ˜≤ÈΩ·π˚ªÊ÷∆◊˜≥…»Áœ¬¡Ω∑˘≤ªÕÍ’˚µƒÕ≥º∆Õº£¨«Îƒ„∏˘æðÕº÷–Ã·π©µƒ–≈œ¢Ω‚¥œ¬¡–Œ £∫
¢≈‘⁄’‚¥Œµ˜≤È÷–“ªπ≤µ˜≤È¡À∂ý…Ÿ√˚—ß…˙£ø
¢∆«ÛªßÕ‚ªÓ∂Ø ±º‰Œ™1.5–° ±µƒ»À ˝£¨≤¢≤π»´∆µ ˝∑÷≤º÷±∑ΩÕº£ª
¢««Û±Ì æªßÕ‚ªÓ∂Ø ±º‰ 1–° ±µƒ…»–Œ‘≤–ƒΩ«µƒ∂» ˝£ª
¢»±æ¥Œµ˜≤È÷–£¨—ß…˙≤Œº”ªßÕ‚ªÓ∂صƒ∆Ωæ˘ ±º‰ «∑Ò∑˚∫œ“™«Û?ªßÕ‚ªÓ∂Ø ±º‰µƒ÷⁄ ˝∫Õ÷–Œª ˝ «∂ý…Ÿ?

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþ![]() ”Îx÷·œýΩª”⁄A£®3£¨0£©°¢B¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£®0£¨3£©£¨µ„B‘⁄x÷·µƒ∏∫∞Î÷·…œ£¨«“
”Îx÷·œýΩª”⁄A£®3£¨0£©°¢B¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£®0£¨3£©£¨µ„B‘⁄x÷·µƒ∏∫∞Î÷·…œ£¨«“![]() .
.
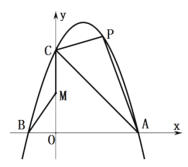

£®1£©«Û≈◊ŒÔœþµƒ∫Ø ˝πÿœµ Ω£ª
£®2£©»ÙP «≈◊ŒÔœþ…œ«“Œª”⁄÷±œþ![]() …œ∑Ωµƒ“ª∂ص„£¨«Û
…œ∑Ωµƒ“ª∂ص„£¨«Û![]() µƒ√ʪ˝µƒ◊Ó¥Û÷µº∞¥À ±µ„Pµƒ◊¯±Í£ª
µƒ√ʪ˝µƒ◊Ó¥Û÷µº∞¥À ±µ„Pµƒ◊¯±Í£ª
£®3£©‘⁄œþ∂Œ![]() …œ «∑ҥʑ⁄“ªµ„M£¨ π
…œ «∑ҥʑ⁄“ªµ„M£¨ π![]() µƒ÷µ◊Ó–°£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆ’‚∏ˆ◊Ó–°÷µº∞∂‘”¶µƒMµ„µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
µƒ÷µ◊Ó–°£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆ’‚∏ˆ◊Ó–°÷µº∞∂‘”¶µƒMµ„µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
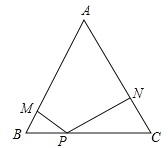
°æƒø°ø£®2017ƒ˛œƒ£©‘⁄±þ≥§Œ™2µƒµ»±þ»˝Ω«–ŒABC÷–£¨P «BC±þ…œ»Œ“‚“ªµ„£¨π˝µ„ P∑÷±◊˜ PM°ÕA B£¨PN°ÕAC£¨M°¢N∑÷±Œ™¥π◊„£Æ
£®1£©«Û÷§£∫≤ª¬€µ„P‘⁄BC±þµƒ∫Œ¥¶ ±∂º”–PM+PNµƒ≥§«°∫√µ»”⁄»˝Ω«–ŒABC“ª±þ…œµƒ∏þ£ª
£®2£©µ±BPµƒ≥§Œ™∫Œ÷µ ±£¨Àƒ±þ–ŒAMPNµƒ√ʪ˝◊Ó¥Û£¨≤¢«Û≥ˆ◊Ó¥Û÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø2018ƒÍ∑«÷Þ÷ÌŒ¡“þ«È±©∑¢∫Û£¨ΩÒƒÍ÷Ì»‚º€∏Ò≤ª∂œ◊þ∏þ£¨“˝∆¡À√Ò÷⁄”Î’˛∏Ƶƒ∏þ∂»πÿ◊¢£¨æðÕ≥º∆£∫ΩÒƒÍ7‘¬20»’÷Ì»‚º€∏Ò±»Ω҃̓Í≥ı…œ’«¡À60%£¨ƒ≥ –√ÒΩÒƒÍ7‘¬20»’‘⁄ƒ≥≥¨ –π∫¬Ú1«ßøÀ÷Ì»‚ª®¡À80‘™«Æ£Æ
£®1£©Œ £∫Ω҃̓Í≥ı÷Ì»‚µƒº€∏ÒŒ™√ø«ßøÀ∂ý…Ÿ‘™£ø
£®2£©ƒ≥≥¨ –Ω´Ω¯ªıº€Œ™√ø«ßøÀ65‘™µƒ÷Ì»‚£¨∞¥7‘¬20»’º€∏Ò≥ˆ €£¨∆Ωæ˘“ªÃσМ˙ €≥ˆ100«ßøÀ£¨æ≠µ˜≤ȱÌ√˜£∫÷Ì»‚µƒ €º€√ø«ßøÀœ¬Ωµ1‘™£¨∆‰»’œ˙ €¡øæÕ‘ˆº”10«ßøÀ£¨≥¨ –Œ™¡À µœ÷œ˙ €÷̃⁄√øÃÏ”–1560‘™µƒ¿˚»Û£¨≤¢«“ø…ƒÐ»√πÀøÕµ√µΩ µªð£¨÷Ì»‚µƒ €º€”¶∏√œ¬Ωµ∂ý…Ÿ‘™£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄µ»±þ°˜ABCƒ⁄”–“ªµ„D£¨AD=5£¨BD=6£¨CD=4£¨Ω´°˜ABD»∆µ„AƒÊ ±’Ζ˝◊™£¨ πAB”ÎAC÷ÿ∫œ£¨µ„D–˝◊™µΩµ„E£¨‘Ú°œCDEµƒ’˝«–÷µŒ™ £Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨’˝∑Ω–ŒABCD÷–£¨MŒ™BC…œ“ªµ„£¨F «AMµƒ÷–µ„£¨EF°ÕAM£¨¥π◊„Œ™F£¨ΩªADµƒ—”≥§œþ”⁄µ„E£¨ΩªDC”⁄µ„N£Æ
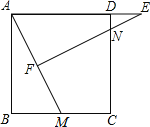
£®1£©«Û÷§£∫°˜ABM°◊°˜EFA£ª
£®2£©»ÙAB=12£¨BM=5£¨«ÛDEµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£∫»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨°˜ABC «÷±Ω«»˝Ω«–Œ£¨°œACB=90°„£¨µ„A£¨Cµƒ◊¯±Í∑÷±Œ™A£®©Å3£¨0£©£¨C£®1£¨0£©£¨tan°œBAC=![]() £Æ
£Æ
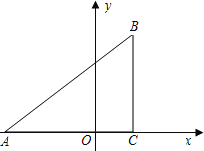
£®1£©«Ûπ˝µ„A£¨Bµƒ÷±œþµƒ∫Ø ˝±Ì¥Ô Ω£ª
£®2£©‘⁄x÷·…œ’““ªµ„D£¨¡¨Ω”BD£¨ πµ√°˜ADB”ΰ˜ABCœýÀ∆£®≤ª∞¸¿®»´µ»£©£¨≤¢«Ûµ„Dµƒ◊¯±Í£ª
£®3£©‘⁄£®2£©µƒÃıº˛œ¬£¨»ÁP£¨Q∑÷± «AB∫ÕAD…œµƒ∂ص„£¨¡¨Ω”PQ£¨…ËAP=DQ=m£¨Œ «∑ҥʑ⁄’‚—˘µƒm πµ√°˜APQ”ΰ˜ADBœýÀ∆£ø»Á¥Ê‘⁄£¨«Î«Û≥ˆµƒm÷µ£ª»Á≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com