
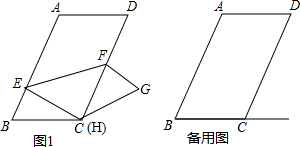
 以正方形ABCD的对角线AC、BD所在直线为坐标轴,建立平面直角坐标系,如图所示,已知点A的坐标是(-$\sqrt{2}$,0),现将正方形ABCD绕原点O顺时针旋转45°,则旋转后点C的对应点坐标是( )
以正方形ABCD的对角线AC、BD所在直线为坐标轴,建立平面直角坐标系,如图所示,已知点A的坐标是(-$\sqrt{2}$,0),现将正方形ABCD绕原点O顺时针旋转45°,则旋转后点C的对应点坐标是( )| A. | ($\sqrt{2}$,$\sqrt{2}$) | B. | ($\sqrt{2}$,-$\sqrt{2}$) | C. | (-1,1) | D. | (1,-1) |
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(件) | … | 5 | 10 | 15 | 20 | … |
| y(元/件) | … | 75 | 70 | 65 | 60 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
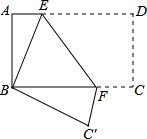 如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )
如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )| A. | 3 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
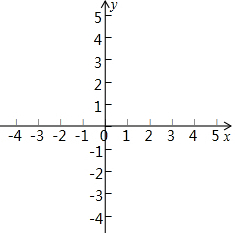 定义:对于平面直角坐标系xOy中的线段PQ和点M,在△MPQ中,当PQ边上的高为2时,称M为PQ的“等高点”,称此时MP+MQ为PQ的“等高距离”.
定义:对于平面直角坐标系xOy中的线段PQ和点M,在△MPQ中,当PQ边上的高为2时,称M为PQ的“等高点”,称此时MP+MQ为PQ的“等高距离”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
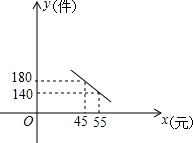 大学生王强积极响应“自主创业”的好种,准备投资销售一种进价为每件4元的小家电,通过试营销发现,当销售单价在40元至60元之间(含40元和60元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.
大学生王强积极响应“自主创业”的好种,准备投资销售一种进价为每件4元的小家电,通过试营销发现,当销售单价在40元至60元之间(含40元和60元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com