分析:作出图形,分①点A是顶点时,根据等腰三角形三线合一的性质可得BD=CD,从而得到AD=BD=CD,再利用等边对等角的性质可得∠B=∠BAD,然后利用直角三角形两锐角互余求解即可;
②点A是底角顶点时,再分AD在△ABC外部时,根据直角三角形30°角所对的直角边等于斜边的一半求出∠ACD=30°,再根据三角形的一个外角等于与它不相邻的两个内角的和求解即可得到底角是15°,AD在△ABC内部时,根据直角三角形30°角所对的直角边等于斜边的一半求出∠C=30°,然后再根据等腰三角形两底角相等求解即可.
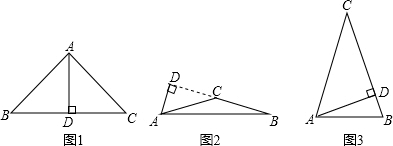
解答:解:①如图1,点A是顶点时,∵AB=AC,AD⊥BC,
∴BD=CD,
∵AD=
BC,
∴AD=BD=CD,
在Rt△ABD中,∠B=∠BAD=
(180°-90°)=45°;
②如图2,点A是底角顶点,且AD在△ABC外部时,
∵AD=
BC,AC=BC,
∴AD=
AC,
∴∠ACD=30°,
∴∠BAC=∠ABC=
×30°=15°;
③如图3,点A是底角顶点,且AD在△ABC内部时,
∵AD=
BC,AC=BC,
∴AD=
AC,
∴∠C=30°,
∴∠BAC=∠ABC=
(180°-30°)=75°;
综上所述,△ABC底角的度数为45°或15°或75°.
点评:本题考查了30°角所对的直角边等于斜边的一半的性质,等腰三角形的两底角相等的性质,以及三角形的一个外角等于与它不相邻的两个内角的和的性质,难点在于要分情况讨论求解.




 阅读快车系列答案
阅读快车系列答案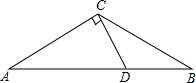 如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.
如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.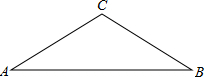 如图,已知在等腰△ABC中,∠ACB=120°.
如图,已知在等腰△ABC中,∠ACB=120°.