
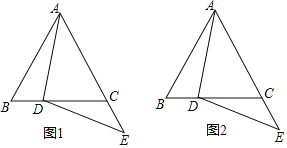
【题目】在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1).
(1)求证:∠BAD=∠EDC;
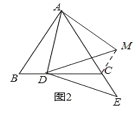
(2)点E关于直线BC的对称点为M,连接DM,AM.
①依题意将图2补全;
②小姚通过观察、实验提出猜想:在点D运动的过程中,始终有DA=AM,小姚把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明DA=AM,只需证△ADM是等边三角形;
想法2:连接CM,只需证明△ABD≌△ACM即可.
请你参考上面的想法,帮助小姚证明DA=AM(一种方法即可).
【答案】(1)见解析(2)见解析
【解析】
(1)根据等腰三角形的性质,得出∠E=∠DAC,根据等边三角形的性质,得出∠BAD+∠DAC=∠E+∠EDC=60°,据此可得出∠BAD=∠EDC;
(2)①根据轴对称作图即可;②要证明DA=AM,只需根据有一个角是60°的等腰三角形是等边三角形,证△ADM是等边三角形即可.
解:(1)如图1,∵DE=DA,
∴∠E=∠DAC,
∵△ABC是等边三角形,
∴∠CAB=∠DCA=60°,
即∠BAD+∠DAC=∠E+∠EDC=60°,
∴∠BAD=∠EDC;
(2)①补全图形如图2;
由轴对称可得,DM=DE,∠EDC=∠MDC,
∵DE=DA,
∴DM=DA,
由(1)可得,∠BAD=∠EDC,
∴∠MDC=∠BAD,
∵△ABD中,∠BAD+∠ADB=180°∠B=120°,
∴∠MDC+∠ADB=120°,
∴∠ADM=180°120°=60°,
∴△ADN是等边三角形,
∴AD=AM.


科目:初中数学 来源: 题型:
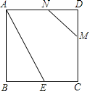
【题目】如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的端点M,N分别在CD,AD上滑动,当DM=______________时,△ABE与以D,M,N为顶点的三角形相似。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校在“你最喜爱的课外活动项目”调查中,随机调查了若干名学生(每名学生分别选了一个活动项目),并根据调查结果绘制了如图所示的扇形统计图.已知“最喜爱机器人”的人数比“最喜爱3D打印”的人数少5人,则被调查的学生总人数为( )

A.50人B.40人C.30人D.25人
查看答案和解析>>
科目:初中数学 来源: 题型:
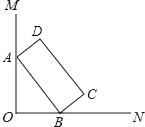
【题目】如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点![]() 不在同一条直线上,
不在同一条直线上,![]()
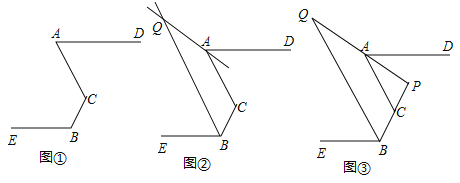
(1)如图①,当![]() 时,求
时,求![]() 的度数;
的度数;
(2)如图②,![]() 分别为
分别为![]() 的平分线所在直线,试探究
的平分线所在直线,试探究![]() 与
与![]() 的数量关系;
的数量关系;
(3)如图③,在(2)的前提下且![]() ,
,![]() ,直接写
,直接写![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,点C是线段AB上一点,点M、N分别是AC、BC的中点.
①若AC=8cm,CB=6cm,请求出线段MN的长;
②若点C满足AC+CB=acm,其它条件不变,你能猜想MN的长度吗?请说明理由;
(2)若C在线段AB的延长线上,且满足AC﹣BC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣3y)(4x﹣3x2﹣1);
(2)(2x+3)(x﹣7);
(3)(-1)2019+(3-π)0 +2-2+ 4101×0.25100;
(4)2019220182020.(运用乘法公式计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行线问题的探索:
(1)问题一:已知:如图,![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 的度数
的度数
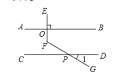
甲、乙.丙三位同学用不同的方法添加辅助线解决问题,如图1:
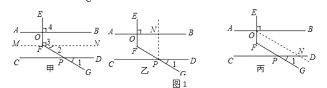
甲同学辅助线的做法和分析思路如下:辅助线:过点![]() 作
作![]() ,分析思路:
,分析思路:
a.欲求![]() 的度数,由图可知只需转化为求
的度数,由图可知只需转化为求![]() 和
和![]() 的度数;
的度数;
b.![]() 可知,
可知,![]() 又由已知
又由已知![]() 的度数可得
的度数可得![]() 的度数;
的度数;
c.由![]() 推出
推出![]() 由此可推出
由此可推出![]() ;
;
d.由已知![]() 可得
可得![]() 所以可得
所以可得![]() 的度数;
的度数;
f.从而可求![]() 的度数
的度数
①请你根据乙同学所画的图形,描述乙同学辅助线的做法.辅助线: _;
②请你根据丙同学所画的图形,且不再添加其他辅助线,求![]() 的度数.
的度数.
(2)问题二: 如图2,在平面直角坐标系中,点![]() 为
为![]() 轴负半轴上一点,点
轴负半轴上一点,点![]() 为
为![]() 轴正半轴上一点,
轴正半轴上一点,![]() 其中
其中![]() 满足关系式:
满足关系式:![]() .
.
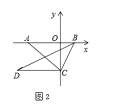
①![]() ,
,![]() ;
;
②根据已知点的坐标判断![]() 与
与![]() 的位置关系是
的位置关系是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1过点A(0,4),点D(4,0),直线l2:![]() 与x轴交于点C,两直线
与x轴交于点C,两直线![]() ,
,![]() 相交于点B.
相交于点B.
(1)求直线![]() 的解析式和点B的坐标;
的解析式和点B的坐标;
(2)求△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com