
分析 (1)把常数项-99移项后,在左右两边同时加上一次项系数的一半的平方,利用配方法即可解得.
(2)找出a,b,c的值,求出b2-4ac>0,代入求根公式即可求出值.
(3)找出a,b,c的值,求出b2-4ac<0,则原方程无实数根;
(4)先把方程左边分解得到(5x-5)(-x+13)=0,原方程转化为5x-5=0或-x+13=0,然后解一次方程即可.
解答 解:(1)x2+2x-99=0(配方法);
x2+2x+1=99+1,
(x+1)2=100,
∴x+1=±10,
∴x1=9,x2=-11;
(2)3x2+x-5=0(公式法);
∵a=3,b=1,c=-5,b2-4ac=1+4×3×5=61,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{-1±\sqrt{61}}{2×3}$=$\frac{-1±\sqrt{61}}{6}$,
∴x1=$\frac{-1+\sqrt{61}}{6}$,x2=$\frac{-1-\sqrt{61}}{6}$;
(3)8x2+15x+20=0(公式法);
∵a=8,b=15,c=20,b2-4ac=225-640<0,
∴原方程无实数根;
(4)4(x+2)2-9(x-3)2a=0(因式分解法).
[2(x+2)+3(x-3)][2(x+2)-3(x-3)]=0,
(5x-5)(-x+13)=0,
∴5x-5=0,-x+13=0,
∴x1=-1,x2=13.
点评 本题考查了解一元二次方程,熟练掌握和运用解一元二次方程的方法是解题的关键.


科目:初中数学 来源: 题型:解答题
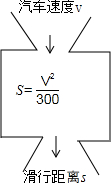 在平整的路面上.某型号汽车紧急刹车后仍将滑行S米,一般地有经验公式S=$\frac{{V}^{2}}{300}$,其中V表示刹车前汽车的速度(单位:千米/时).
在平整的路面上.某型号汽车紧急刹车后仍将滑行S米,一般地有经验公式S=$\frac{{V}^{2}}{300}$,其中V表示刹车前汽车的速度(单位:千米/时).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| +7 | +5 | -4 | +6 | +4 | +3 | -3 | -2 | +8 | +1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | -7 | -6 | -5 | -4 | -3 | -2 |
| y | -27 | -13 | -3 | 3 | 5 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
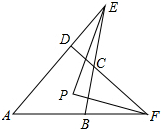 四边形ABCD中,AD、BC的延长线交于E,AB、DC的延长线交于F,∠AEB、∠AFD的平分线交于点P,∠A=64°,∠BCD=136°.
四边形ABCD中,AD、BC的延长线交于E,AB、DC的延长线交于F,∠AEB、∠AFD的平分线交于点P,∠A=64°,∠BCD=136°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com