
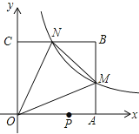
【题目】如图,在平面直角坐标系中,反比例函数![]() 的图象与边长是6的正方形OABC的两边AB、BC分别相交于M、N两点,△OMA的面积为6.
的图象与边长是6的正方形OABC的两边AB、BC分别相交于M、N两点,△OMA的面积为6.
(1)求反比例函数![]() 的解析式;
的解析式;
(2)若动点P在x轴上,求PM+PN的最小值.
【答案】(1)y=![]() ;(2)4
;(2)4![]()
【解析】
(1)由正方形OABC的边长是6,得到点M的横坐标和点N的纵坐标为6,求得M(6,![]() ),根据三角形的面积求得k的值;
),根据三角形的面积求得k的值;
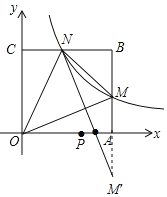
(2)作M关于x轴的对称点M′,连接NM′交x轴于P,则NM′的长=PM+PN的最小值,根据勾股定理即可得到结论.
解:(1)∵正方形OABC的边长是6,
∴点M的横坐标和点N的纵坐标为6,
∴M(6,![]() ),N(
),N(![]() ,6),
,6),
∵△OMA的面积为6,
∴![]() ×6×
×6×![]() =6,
=6,
∴k=12,
∴反比例函数y=![]() (x>0,k≠0)的解析式为y=
(x>0,k≠0)的解析式为y=![]() ;
;
(2)由y=![]() 可得M(6,2)和N(2,6),作M关于x轴的对称点M′,
可得M(6,2)和N(2,6),作M关于x轴的对称点M′,
∴AM=AM′=2,连接NM′交x轴于P,则M′N的长等于PM+PN的值最小,
∵AB=6,
∴BM′=8,BN=4,根据勾股定理求得NM′=![]() =4
=4![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
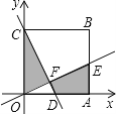
【题目】如图,在直角坐标系中,正方形OABC顶点B的坐标为(6,6),直线CD交直线OA于点D,直线OE交线段AB于点E,且CD⊥OE,垂足为点F,若图中阴影部分的面积是正方形OABC的面积的![]() ,则△OFC的周长为______.
,则△OFC的周长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式,能够表示图中阴影部分的面积的是( )
①ac+(b﹣c)c;②ac+bc﹣c2;③ab﹣(a﹣c)(b﹣c);④(a﹣c)c+(b﹣c)c+c2

A. ①②③④ B. ①②③ C. ①② D. ①
查看答案和解析>>
科目:初中数学 来源: 题型:
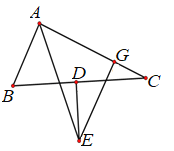
【题目】如图,在△ABC中,AE为∠BAC的角平分线,点D为BC的中点,DE⊥BC交AE于点E,EG⊥AC于点G.
(1)求证: AB+AC=2AG.
(2)若BC=8cm,AG=5cm,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用的练习本可在甲、乙两个商店买到.已知两个商店的标价都是每本1元,但甲商店的优惠条件是:购买10本以上,从第11本开始按标价的七折卖;乙商店的优惠条件是:从第一本开始就按标价的八五折卖.小明要买18个练习本,到__________商店买较省钱;小明现有24元,最多可买__________本练习本.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B两点的坐标分别为(40,0)和(0,30),动点P从点A开始在线段AO上以每秒2个长度单位的速度向原点O运动、动直线EF从x轴开始以每秒1个单位的速度向上平行移动(即EF∥x轴),并且分别与y轴、线段AB交于点E、F,连接EP、FP,设动点P与动直线EF同时出发,运动时间为t秒.
(1)求t=15时,△PEF的面积;
(2)直线EF、点P在运动过程中,是否存在这样的t,使得△PEF的面积等于160(平方单位)?若存在,请求出此时t的值;若不存在,请说明理由.
(3)当t为何值时,△EOP与△BOA相似.

查看答案和解析>>
科目:初中数学 来源: 题型:
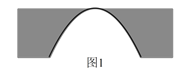
【题目】河上有一座桥孔为抛物线形的拱桥(如图 ![]() ),水面宽
),水面宽 ![]() 时,水面离桥孔顶部
时,水面离桥孔顶部 ![]() ,因降暴雨水面上升
,因降暴雨水面上升 ![]() .
.
(1)建立适当的坐标系,并求暴雨后水面的宽;(结果保留根号)
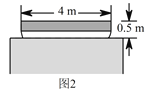
(2)一艘装满物资的小船,露出水面的部分高为 ![]() ,宽
,宽 ![]() (横断面如图
(横断面如图 ![]() 所示),暴雨后这艘船能从这座拱桥下通过吗?
所示),暴雨后这艘船能从这座拱桥下通过吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市努力改善空气质量,近年来空气质量明显好转,根据环境保护局公布的2006-2010这五年各年的全年空气质量优良的天数,绘制折线图如图.根据图中信息回答:
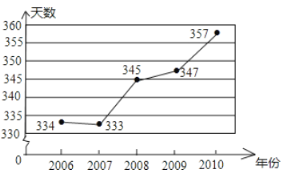
(1)这五年的全年空气质量优良天数的中位数是 ,极差是 .
(2)求这五年的全年空气质量优良天数的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了![]() 两种上网学习的月收费方式.
两种上网学习的月收费方式.
收费方式 | 月使用费/元 | 包时上网时间/ | 超时费/(元/ |
| 12 | 40 | 0.5 |
|
|
| 0.6 |
设每月上网学习时间为![]() 小时,方案
小时,方案![]() 的收费金额分别为
的收费金额分别为![]() ,
,![]() .
.
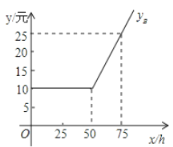
(1)如图是![]() 与
与![]() 之间的函数关系图象,请根据图象填空:
之间的函数关系图象,请根据图象填空:![]() = ;
= ;![]() =
=
(2)求出![]() 与
与![]() (
(![]() )之间的函数关系式.
)之间的函数关系式.
(3)如果每月上网时间为60小时,选择哪种方式网上学习合算,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com