
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��y��kx+b(k��0)��������(6��0)������������Χ�ɵ������ε������9���뺯��y��![]() (x��0)��ͼ��G����A��B���㣮
(x��0)��ͼ��G����A��B���㣮
(1)��ֱ�ߵı���ʽ��
(2)�ᡢ�����궼�������ĵ�������㣮��ͼ��G�ڵ�A��B֮��IJ������߶�ABΧ�ɵ�����(�����߽�)ΪW��
����m��2ʱ��ֱ��д������W�ڵ������������ ����
��������W��ǡ��3�������㣬��Ϻ���ͼ����m��ȡֵ��Χ��

���𰸡�(1)y����![]() x+3��(2)��(3��1)����1��m��2��
x+3��(2)��(3��1)����1��m��2��
��������
��1������ֱ����x�ᡢy��Ľ��������ʾ��ֱ����������Χ�ɵ������ε�����ֱ�DZ߳������������9�����ֱ����y��Ľ���ΪC��0��3�������ô���ϵ�������ֱ�ߵı���ʽ��
��2�����������m=2ʱ��������ͼ��Ľ������꣬�ٽ��ͼ���ҵ�����W�ڵ���������ꣻ����������ֵ�����ͼ���㣨1��1������2��1��ʱ��������������m��ֵ�����ͼ��õ��ڴ˷�Χ������W��������3�����Ӷ�ȷ��m��ȡֵ��ΧΪ1��m��2��
��ͼ��
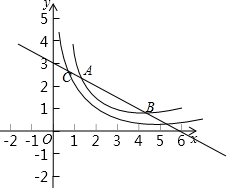
��1����ֱ����y��Ľ���ΪC(0��b)��
��ֱ������������Χ�ɵ������ε������9��
��![]() ��6
��6![]() ��9��b����3��
��9��b����3��
��k��0��
��b��3��
��ֱ��y��kx+b������(6��0)��(0��3)��
��ֱ�ߵı���ʽΪy����![]() x+3��
x+3��
��2���ٵ�m��2ʱ��������ͼ��Ľ�������Ϊ������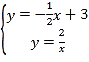 �Ľ⣬
�Ľ⣬
��A(3��![]() ��
��![]() )��B(3+
)��B(3+![]() ��
��![]() )���۲�ͼ��ɵ�����W�ڵ����������Ϊ(3��1)��
)���۲�ͼ��ɵ�����W�ڵ����������Ϊ(3��1)��
�ڵ�y��![]() ͼ����(1��1)ʱ���� m��1��
ͼ����(1��1)ʱ���� m��1��
��y��![]() ͼ����(2��1)ʱ���� m��2��
ͼ����(2��1)ʱ���� m��2��
��۲�ͼ��ɵ�����W�ڵ�������3��ʱ1��m��2��


 ��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��
��1����ͼ1��E��G�ֱ���OB��OC�ϵĵ㣬CE��DG���ӳ����ཻ�ڵ�F����DF��CE����֤��OE=OG��
��2����ͼ2��H��BC�ϵĵ㣬����H��EH��BC�����߶�OB�ڵ�E������DH��CE�ڵ�F����OC�ڵ�G����OE=OG��
����֤����ODG=��OCE��
�ڵ�AB=1ʱ����HC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ͼ��![]() ��ͼ��
��ͼ��![]() �ϵ�����
�ϵ�����![]() ��
��![]() �����
�����![]() �ϵ����е㶼��ͼ��
�ϵ����е㶼��ͼ��![]() ���ڲ�����ϣ����
���ڲ�����ϣ����![]() Ϊͼ��
Ϊͼ��![]() ���ڻ����ر�ģ���
���ڻ����ر�ģ���![]() �У�
��![]() ��
��![]() �ֱ���
�ֱ���![]() ���ߵ��е㣬���
���ߵ��е㣬���![]() �ϵ����е㶼��
�ϵ����е㶼��![]() ���ڲ�����ϣ����
���ڲ�����ϣ����![]() Ϊ
Ϊ![]() �����ڻ�����ע��
�����ڻ�����ע��![]() ��ָ�ӻ����Բ����ƽ��ֱ������ϵ�У���֪��
��ָ�ӻ����Բ����ƽ��ֱ������ϵ�У���֪��![]()
![]() �����ڻ�����Բ��Բ��Ϊ
�����ڻ�����Բ��Բ��Ϊ![]() ��
��
��1����![]() ʱ������
ʱ������![]() ��
��![]() ���ӳ���
���ӳ���
������ͼ1�л���һ��![]() ���ڻ�
���ڻ�![]() ��
��
����ֱ��д��![]() ���ڻ�
���ڻ�![]() ���ȵ����ֵ__________��
���ȵ����ֵ__________��
��2������![]() ��
��![]() ���ӳ���
���ӳ���
�ٵ�![]() ʱ����ֱ��д��
ʱ����ֱ��д��![]() �������ڻ�
�������ڻ�![]() ����Բ��Բ��
����Բ��Բ��![]() ���������ȡֵ��Χ__________��
���������ȡֵ��Χ__________��
����ֱ��![]() �ϴ���
�ϴ���![]() ���ڻ�
���ڻ�![]() ����Բ��Բ��
����Բ��Բ��![]() �������
�������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3������![]() ���ڵ�
���ڵ�![]() �ĶԳƵ�
�ĶԳƵ�![]() ������
������![]() ���ڵ�
���ڵ�![]() �ĶԳƵ�
�ĶԳƵ�![]() ������
������![]() ��
��![]() ��
��![]() ����
����![]() ����
����![]() �����ڻ�
�����ڻ�![]() ���ڵ�Բ��Բ��
���ڵ�Բ��Բ��![]() ��
��![]() ���ⲿʱ��
���ⲿʱ��![]() ���������ڻ�
���������ڻ�![]() �����ڣ���ֱ��д��
�����ڣ���ֱ��д��![]() ��ȡֵ��Χ__________��
��ȡֵ��Χ__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
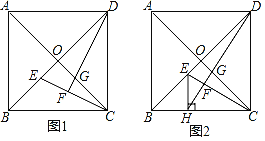
����Ŀ����ͼ���ı���OABC�Ǿ��Σ�A��C�ֱ���y�ᡢx���ϣ���OA��6cm��OC��8cm����P�ӵ�A��ʼ��2cm/s���ٶ���B�˶�����Q�ӵ�B��ʼ��1cm/s���ٶ���C�˶������˶�ʱ��Ϊt��
��1����ͼ��1������tΪ��ֵʱ����BPQ�����Ϊ4cm2��
��2����tΪ��ֵʱ����B��P��QΪ���������������ABC���ƣ�
��3����ͼ��2�������˶������е�ijһʱ�̣�����������y��![]() ��ͼ��ǡ��ͬʱ����P��Q���㣬����������������Ľ���ʽ��
��ͼ��ǡ��ͬʱ����P��Q���㣬����������������Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������һ����Ҫ�����۷�ʽ��ij����ũó��˾�¿�����һ�����꣬���۵���ũ��Ʒ������һ�ֵ����ز������������ۣ���ɱ�Ϊÿǧ��10Ԫ����˾���������ڼ䣬���鷢�֣�ÿ��������y��kg�������۵���x��Ԫ��������ͼ��ʾ�ĺ�����ϵ������![]() ����
����
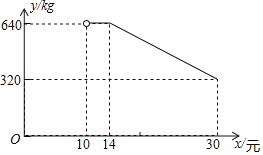
��1��ֱ��д��y��x֮��ĺ�����ϵʽ���Ա�����ȡֵ��Χ��
��2����ũó��˾ÿ�����۸��ز�������Ҫ�ﵽ3100Ԫ�������۵���xӦ��Ϊ����Ԫ��
��3����ÿ�����۸��ز�������ΪWԪ����![]() �������۵���xΪ����Ԫʱ��ÿ����������������������Ƕ���Ԫ��
�������۵���xΪ����Ԫʱ��ÿ����������������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵ�е�����һ��![]() ���Ƕ��壺��
���Ƕ��壺��![]() Ϊ��������
Ϊ��������![]() ʱ����
ʱ����![]() Ϊ��
Ϊ��![]() �ġ�
�ġ�![]() ��Ӧ�㡱��
��Ӧ�㡱��
��1����![]() �ġ�
�ġ�![]() ��Ӧ�㡱
��Ӧ�㡱![]() ������Ϊ��������������
������Ϊ��������������![]() �ġ�
�ġ�![]() ��Ӧ�㡱
��Ӧ�㡱![]() ������Ϊ
������Ϊ![]() ���ҵ�
���ҵ�![]() ��������Ϊ
��������Ϊ![]() �����
�����![]() �����
�����![]() ����������
����������
��2������![]() �ġ�
�ġ�![]() ��Ӧ�㡱
��Ӧ�㡱![]() �ڵ�һ�������Ľ�ƽ����(ԭ�����)�ϣ���
�ڵ�һ�������Ľ�ƽ����(ԭ�����)�ϣ���![]() ֵ��
ֵ��
��3������![]() ��
��![]() ��ĸ������ϣ���
��ĸ������ϣ���![]() �ġ�
�ġ�![]() ��Ӧ�㡱Ϊ
��Ӧ�㡱Ϊ![]() �㣬��
�㣬��![]() ����
����![]() ֵ��
ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������С��ͬѧ��Ƶ�����ֱ����һ������ֱ֪�ߵ�ƽ�������ij߹���ͼ���̣�

��֪����ͼ��ֱ��![]() ��ֱ��
��ֱ��![]() ��һ��
��һ��![]() ������ֱ��
������ֱ��![]() ��ʹ��
��ʹ��![]()
��������ͼ
����ֱ��![]() ����ȡһ��
����ȡһ��![]() ���Ե�
���Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶��Բ����ֱ��
Ϊ�뾶��Բ����ֱ��![]() ���ڵ�
���ڵ�![]() ��
��![]() ����
����
������![]() ��
��![]() ���ӳ�
���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]()
����![]() ��ƽ����
��ƽ����![]() ���������ӳ�
���������ӳ�
����ֱ��![]() ������������ֱ��
������������ֱ��
����С��ͬѧ��Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ�������ͼ�ۼ���
��2����������֤��
֤����![]() ��
��
![]() (_______________________)(������������)
(_______________________)(������������)
![]() ��
��![]() �����
�����
![]() ��
��
![]() ƽ��
ƽ��![]() __________________
__________________
![]() (____________________)(������������)
(____________________)(������������)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�У�AC��BD�ཻ�ڵ�O����E��OA���е㣬����BE���ӳ���AD�ڵ�F��S��AEF��4�������н��ۣ���FD��2AF����S��BCE��36����S��ABE��16�� ����AEF�ס�ACD������һ����ȷ���ǣ�������

A.�٢ڢۢ�B.�٢�C.�ڢۢ�D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AC=5cm����BAC=60��������M�ӵ�B��������BA������ÿ��2cm���ٶ����A�����˶���ͬʱ����N�ӵ�C��������CB������ÿ��![]() cm���ٶ����B�����˶������˶�ʱ��Ϊt�루0��t��5��������MN��
cm���ٶ����B�����˶������˶�ʱ��Ϊt�루0��t��5��������MN��
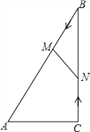
��1����BM=BN����t��ֵ��
��2������MBN���ABC���ƣ���t��ֵ��
��3����tΪ��ֵʱ���ı���ACNM�������С���������Сֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com