
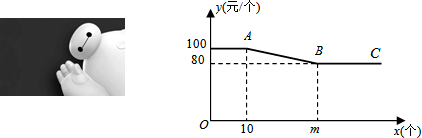
分析 (1)利用价格变化规律,进而求出m的值,然后根据解析式解释线段AB所表示的实际优惠销售政策即可;
(2)分类讨论:当0<x≤10时,当10<n≤30时;当n>30时,分别得出等式;
(3)配方W=-x2+50x得到W=-(x-25)2+625,根据二次函数的性质讨论增减性,可得卖25个赚的钱反而比卖30个赚的钱多.为了不出现这种现象,在其他条件不变的情况下,店长应把最低价每个80元至少提高到85元.
解答 解:(1)由题意可得:m=(100-80)+10=30,
射线BC所表示的实际意义是:当一次销售数量超过30个以后,都是按单价80元/个销售;
(2)当0<x≤10时,
w=(100-60)x=40x,
当10<x≤30时,y=100-(x-10)=110-x,
w=[100-(x-10)-60]x=-x2+50x,
当x>30时,w=(80-60)x=20x;
(3)当10<x≤30时,w=-x2+50x=-(x-25)2+625.
①当10<x≤25时,w随x的增大而增大,即卖的个数越多,利润越大.
②当25<x≤30时,w随x的增大而减小,即卖的个数越多,利润越小.
当x=25时,售价为y=110-x=85(元).
故为了不出现这种现象,在其他条件不变的情况下,店家应把最低价每个80元至少提高到每个85元.
点评 本题考查了二次函数的应用:先得到二次函数的顶点式y=a(x-h)2+k,当a<0,x=h时,y有最大值k;当a>0,x=h时,y有最小值k;也考查了二次函数的增减性以及利用待定系数法求函数的解析式.熟练的运用二次函数的增减性质是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
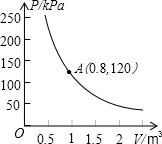 某气球内充满了一定质量的气体,当温度不变时,气球内的气压p(kpa)是气体体积v(m3)的反比例函数,其图象如图所示.
某气球内充满了一定质量的气体,当温度不变时,气球内的气压p(kpa)是气体体积v(m3)的反比例函数,其图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
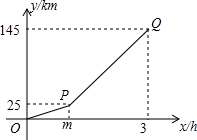 甲、乙两地相距145km,小李骑摩托车从甲地出发去往乙地,速度为25km/h,中途因故换成汽车继续前往乙地(换车时间忽略不计),小李与甲地的距离y(单位:km)和所用时间x(单位:h)之间的关系如图所示.
甲、乙两地相距145km,小李骑摩托车从甲地出发去往乙地,速度为25km/h,中途因故换成汽车继续前往乙地(换车时间忽略不计),小李与甲地的距离y(单位:km)和所用时间x(单位:h)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购买件数 | 销售价格 |
| 不超过30件 | 单价40元 |
| 超过30件 | 每多买1件,购买的所有衬衫单价降低0.5元,但单价不得低于30元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com